Forum de Mathématiques: Maths-Forum

merci et je trouve pour l'instant :


me suis-je trompé en dérivant ? :mur:

Bonjour, pourriez-vous me donner une piste à ce problème J'ai essayé avec le raisonnement par récurrence mais en vain. une fonction f, sa dérivée est notée f(2) , puis la dérivée de la dérivée est notée f(3) , ainsi jusqu'à n f(x) = x^2e^-^x Montrer que pour tout n on a : f(n)...

oui donc ça me donne
et donc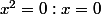
et je devrais trouver x= environ 0.3
mais comment je fais pour la résoudre la 2e partie ?

....l'un des 2 facteurs est nul mais je factorise quoi par ?

bonjour, j'aimerais résoudre l'équation x^2 e^{x-1} - \frac{x^2}{2} =0 pour trouver les abscisses des points d'intersection de cette formule avec l'axe des abscisses d'après moi c'est égal à x^2e^{x-1} = \frac{x^2}{2} je poserais la variable X = \frac{x^2}{2} ce qui revient à : 2X e^{x-1} = X 2X e^{...

quelqu'un pourrait me répondre svp ?

et j'aurais une 2e question et ce sera la dernière : déterminer les abscisses des pts d'intersection de cf avec l'axe des abscisses donc


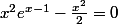
comment puis-je faire ? (je n'attend pas que vous me donniez la réponse mais juste une piste)

c bon merci j'ai trouvé : je trouve un résultat de la sorte
et comme g(x) = 0 le résultat est nul et donc les 2 fonctions sont égales

c'est bien cela ?

je trouve donc

oui mais g(a) =0

et g(x) = (x+2) * e(x-1) - 1

oui dsl g(a)=0

il faut démontrer que x² * e (x-1) - (x²/2) =
- x^3
_____
2(x+2)





dsl je me rend compte qu'en effet c'était mal formulé
et dans e (x-1), x-1 est en exposant

Bonjour, je suis bloqué à une question, et bien qu'en apparence simple je n'y arrive pas, voici l'énoncé : (e est bien sur la fonction exponentielle :zen: ) f(x) = x² e(x-1) - (x²/2) on sait que que alpha (a) est compris entre 0.20 et 0.21 démontrer que f(alpha) = - a^3 2(x+2) en mettant f(X) au mem...