Forum de Mathématiques: Maths-Forum

l'ennui est qu'il y a 2 inconnues... je peux faire quoi pour me débloquer?

une idée svp ? je suis bloquée pour la suite de l'exercice...

merci , c'est déjà mieux ! j'obtiens : f-g= (1+x)^n - (1+nx) est-ce utile et possible de développer la fonction obtenue ? en effet , je dois ensuite étudier les variations de f-g ; je calcule les dérivées et j'ai alors : f'(x)= n (1+x)^{n-1} g'(x)= n d...

bonjour, f_n (x) = (1+x)^n on me demande de terminer la tangente T de f (d'équation g) en O et j'ai obtenu g = 1^n + n (1)^{n-1} x cela vous semble juste ? je dois étudier ensuite le signe de f-g je ne sais pas si l'équation de laquelle je pars est bonne ni comment étudier le...

ça me revient , merci

(le signe sous limite signifie , tend vers + infini )

une autre question me pose problème :

je dois démontrer que la droide D d'équation y = x-2 est asymtote à Cf en + infini

soit f(x) =

la formule est la suivante :

merci , je vais essayer de continuer !

la dérivée est , d'après mes calculs (...) la suivante :
f ' (x) =

bonsoir , je n'arrive pas à trouver le signe de f ' (x) sur ]1 ; +infini [
(duquel je dois déduire le tableau de variation de f )
avec f(x) =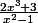

pourriez vous m'aider ? c'est assez urgent , et le reste de l'exercice dépend de cette question , merci de votre aide !

c'est vrai , merci !

mais je tombe sur une forme indéterminée puisque le dénominateur est égal à 0 ;

j'ai aussi essayé = mais je ne vois pas à quoi ça m'avance...

avez-vous une autre idée ?

bonjour ,
je ne parviens pas à trouver la limite en 1 de la fonction
f(x)= définie sur ]1 ; + [

pourriez-vous m'aider ?

j'obtiens :

2x+ racine de(4x²-x+5) = (x-5) / ( 2x- racine de ( 4x²-x+5)

ce qui ne me permet pas de trouver une limite en moins l'infini, encore une forme indéterminée...
à moins que je me sois trompée ?

je vais essayer l'expression conjuguée , je n'y avais pas pensé ,
merci !

bonjour , je ne parviens pas à résoudre une question , pourriez vous m'aider ? (pour que mon énoncé soit compréhensible , comment faire les racines carrées , signe infini ... sur le clavier ?) soit f la fonction définie sur R par f(x)= 2x + racine de (4x²-x+5) C sa courbe représentative. je dois dém...

merci , mais est-il possible de trouver une formule où n'apparaissent plus V(n) et U(n) ?
( y compris V(O) )

bonjour , pourriez-vous m'aider à répondre à la question suivante? on sait que la suite U(n) est définie par U(n+1) = 2U(n)-1 et U(0)=2 on sait également que : V(n)=U(n)-1 je trouve grâce à ces données que V(n) est une suite géométrique : V(n+1)=2 V(n) on me demande ensuite d'en déduire une expressi...

eureka ! merci beaucoup !

j'arrive au système suivant :

2x-4y=0
4x+4y=0

x et y seraient du vecteurs IJ seraient nuls ?

en associant les vecteurs IA + AC +CJ , on arrive de toute façon à IJ , je ne vois pas comment ça peut m'aider à me débarrasser des coordonnées inconnues?