Forum de Mathématiques: Maths-Forum

En effet c'est une erreur, on a bien utilisé l'expression avec le + en td.
Merci !

Salut, cela faisait bien longtemps que je ne manipulait plus ces fameuses valeurs propres alors forcément j'ai oublié pas mal de choses. Donc j'ai une petite question, j'ai une matrice triangulaire 3x3, j'ai une valeur propre simple et une valeur propre double. Ma question porte sur le vecteur propr...

Salut, je doute fortement(de ma logique) sur l'exo que voici : Soit g la fonction définie sur l'ensemble des application de ]0;+ \infty [ dans R, par pour tout x réel strictement positif : g(f)(x) = f(x+1)-f(x). Il me faut montrer que le sev constitué des applications polynômiales est stable par g. ...

Ok pour la dérivabilité (et continuité).
Pour la continuité de la dérivée en 0 : DL?

Bonsoir à tous, j'ai un soucis pour résoudre l'exo que voici : i) Trouver a et b réels tels que \int_0^\pi (at + bt²)cos(nt)dt = 1/n² Ça c'est bon grâce à une double IPP. ii) Montrer que \int_0^\pi \! (at+bt^2)\frac{sin(\frac{2n+1}{2}t)}{sin(t/2)} \, dt. -> 0 lorsque n tend v...

:marteau: :marteau:

J'espère que c'est pas censé être trouvable facilement...parce que je ne trouve pô :zen:

Oui pardon pour le f(0) j'étais allé vite.

Pour la somme je trouve qu'elle est égale à (e-e(-1)) , j'espère ne pas m'être planté , je vais me pencher sur la deuxième.

Merci déjà pour le raisonnement.
Bon pour le cas x=0, on a f(0) = (/2)e si je ne me trompe pas ?
En revanche, je galère pour calculer ces sommes plus compliquées...

Salut, j'ai un problème pour terminer l'exo que voici : On pose f(x) = \sum_{n=0}^{\infty}\frac{arccos(cos nx)}{n!}\ J'ai d'abord montré qu'elle est définie sur R, continue, paire et 2-pi périodique. On me demande ensuite de calculer f(0), f( \pi ) , f( \pi /2 ) C'est la que je n'y arrive pa...

Ok en montrant qu'elle converge normalement on montre uniformément, c'est plus logique donc de chercher la normalité avant.
Je suis à la recherche d'une série réelle à termes positifs qui converge. Le sup me dérange quelque peu...

Bonsoir à tous, j'ai un soucis pour résoudre un exo: Je dois étudier la série de terme général fn = 1/sh(nx) avec n entier naturel. Je trouve le domaine de définition qui est R privé de 0. Ensuite j'étudie la convergence simple, en utilisant les équivalent sur sh notamment je parviens à montrer qu'e...

On m'a suggéré de montrer que :
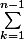
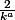est équivalent à

Je n'arrive pas à le montrer très rigoureusement, help!
Avec ce résultat j'arriverais enfin à bout de cet exo.
merci en tout cas!

Ok merci je vois.

Une idée pour un équivalent de Un lorsque la suite ne converge pas?

alavacommejetepousse a écrit:bonjour

on a plutôt comme équivalent

Merci
Comment le trouve-t-on?

Salut, j'ai un soucis sur un exo que voici : Soit a > 0,U1 > 0, on définit la suite (Un) par : Un+1 = Un + \frac{1}{n^aUn} Dans la première question il m'était demandé de déterminer les valeurs de a pour lesquelles la suite converge, j'ai trouvé qu'il fallait avoir a > 1 à partir de la transformatio...

Salut, je bloque sur une démonstration à faire : E un C-espace vectoriel de dimension finie.Soient u et v deux endomorphismes de E tels que u(v) = v(u). Montrer que u et v ont au moins un vecteur propre commun. J'ai essayé d'écrire l'expression d'un vecteur propre de l'un des deux endomorphismes pui...

Bonsoir, j'ai un petit soucis sur l'exo suivant : n un entier naturel non nul, calculer le déterminant d'ordre n suivant : http://nsa09.casimages.com/img/2009/09/20/mini_090920071442926297.jpg Pour résoudre j'éssaye : C1<-C1-Cn C2<-C2-Cn . . . C(n-1)<-C(n-1)-Cn Sauf que je ne trouve rien d'intéressa...

Salut, j'ai un petit soucis qui m'ennuie sur l'exo que voici : E un K espace vectoriel de dimension finie n supérieur ou égal à 1, et f un endomorphisme fixé de E.Pour tout k entier naturel, N k =Ker(f ^k ) ,n k = DimN k ) et I k =Imf ^k ) . La quéstion est de montrer que (N k ) k et (I k ) k sont r...

Déjà le degré de P devrait être clair ( c'est 3 ;) ) en regardant juste le monôme de plus haut degré. Ensuite tu remplaces et tu identifies (méthode bœuf qui marche). Une dernière chose, le fait que P soit de degré 3 me parait logique, sauf qu'on me demande de justifier...Il y a une vrai justificat...

Ok j'ai appliqué la méthode "bourrin" merci.
Par contre la méthode de la somme ca m'intéresse, mais je n'arrive pas à comprendre le pourquoi du comment?