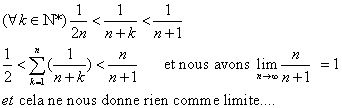Salut,
On a deux fonctions f:I->R g:I->R continues ,
Comment prouver qu'il existe le max(f(x),g(x))??
Aussi comment peut-on prouver cette égalité:
max(f(x),g(x))=1/2|f(x)-g(x)|+1/2(f(x)+g(x)) ??
Je m'y suis suffisamment cassée la tête :mur:
D'aide,SVP!
Merci d'avance!
32 résultats trouvés
Revenir à la recherche avancée
- 14 Déc 2008, 19:18
- Forum: ✯✎ Supérieur
- Sujet: Démo de l'expression du max(f(x),g(x))
- Réponses: 1
- Vues: 3769
Salut, Au fait , j'ai eu la réponse , c'est comme ce qui suit: On veut démontrer que ~qlq soit x et y , il existe r tq: x<y=>x<r ~prenons p=E(n.y) ( comment on a eu l'idée de considérer un nous élément p et de lui donner une telle epression?? :hein: ) Donc p/n=<y<(p+1)/n ~Prenons r=(p-1)/n ( comment...
- 22 Oct 2008, 00:53
- Forum: ✯✎ Supérieur
- Sujet: Entre deux nombre réels , il existe un nombre rationnel ....démonstration?
- Réponses: 6
- Vues: 9039
Entre deux nombre réels , il existe un nombre rationnel ....démonstration?
Salut,
J'arrive pas à démontrer ce qui suit:
Quelque soit x et y appartenant à l'ensemble des nombres réels R, tq x
Merci d'avance!!
J'arrive pas à démontrer ce qui suit:
Quelque soit x et y appartenant à l'ensemble des nombres réels R, tq x
Merci d'avance!!
- 16 Oct 2008, 03:32
- Forum: ✯✎ Supérieur
- Sujet: Entre deux nombre réels , il existe un nombre rationnel ....démonstration?
- Réponses: 6
- Vues: 9039
- 03 Avr 2008, 21:03
- Forum: ✎✎ Lycée
- Sujet: Calcul de la dérivé d'une intégral...
- Réponses: 7
- Vues: 2158
- 03 Avr 2008, 20:39
- Forum: ✎✎ Lycée
- Sujet: Calcul de la dérivé d'une intégral...
- Réponses: 7
- Vues: 2158
- 03 Avr 2008, 19:54
- Forum: ✎✎ Lycée
- Sujet: Calcul de la dérivé d'une intégral...
- Réponses: 7
- Vues: 2158
- 03 Avr 2008, 17:43
- Forum: ✎✎ Lycée
- Sujet: Calcul de la dérivé d'une intégral...
- Réponses: 7
- Vues: 2158
- 03 Avr 2008, 17:26
- Forum: ✎✎ Lycée
- Sujet: calcul de limite
- Réponses: 6
- Vues: 714
Bonsoir,
J'avais le même souci mais d'un autre coté :
A cette étape : pour x = 1/4 : e^(i.pi/2) = 1
on a Ln(e^(i.pi/2))=0
->i.pi/2=0
->i=0
->i²=0
->-1=0
->??????????????
Mais à quelle étape, on a pas respecté les conditions ???
Merci
J'avais le même souci mais d'un autre coté :
A cette étape : pour x = 1/4 : e^(i.pi/2) = 1
on a Ln(e^(i.pi/2))=0
->i.pi/2=0
->i=0
->i²=0
->-1=0
->??????????????
Mais à quelle étape, on a pas respecté les conditions ???
Merci
- 31 Mar 2008, 01:56
- Forum: ✎✎ Lycée
- Sujet: enigme, exponnentielle
- Réponses: 4
- Vues: 680
- 28 Mar 2008, 21:30
- Forum: ✎✎ Lycée
- Sujet: calcul de limite
- Réponses: 6
- Vues: 714
calcul de limite
hola,
merci d'essayer à m'aider à calculer cette limite
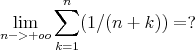
Bonne soirée
merci d'essayer à m'aider à calculer cette limite
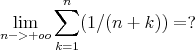
Bonne soirée
- 28 Mar 2008, 19:57
- Forum: ✎✎ Lycée
- Sujet: calcul de limite
- Réponses: 6
- Vues: 714
- 18 Oct 2007, 14:14
- Forum: ✎✎ Lycée
- Sujet: la convergence
- Réponses: 2
- Vues: 383
- 18 Oct 2007, 14:11
- Forum: ✎✎ Lycée
- Sujet: La Loi d'Hôpital
- Réponses: 4
- Vues: 1190
- 17 Oct 2007, 16:58
- Forum: ✎✎ Lycée
- Sujet: La Loi d'Hôpital
- Réponses: 4
- Vues: 1190
........... et si le rapport \frac{f^,(x)}{g^,(x)} admet une limite finie ou égale à +\infty en a , alors : \lim_{x \to a}\frac{f(x)}{g(x)}=\lim_{x \to a}\frac{f^,(x)}{g^,(x)} et pour -oo?? une autre chose,est il toléré d'utiliser cette règle en TS???...
- 16 Oct 2007, 13:43
- Forum: ✎✎ Lycée
- Sujet: La Loi d'Hôpital
- Réponses: 4
- Vues: 1190
La Loi d'Hôpital
Bonjour,
Quelles sont les condition d'utilisation de "Les Lois d'Hôpital"/Hospital rules???
Merci
Quelles sont les condition d'utilisation de "Les Lois d'Hôpital"/Hospital rules???
Merci
- 15 Oct 2007, 22:58
- Forum: ✎✎ Lycée
- Sujet: La Loi d'Hôpital
- Réponses: 4
- Vues: 1190
- 15 Oct 2007, 21:16
- Forum: ✎✎ Lycée
- Sujet: valeur intermédiaire
- Réponses: 7
- Vues: 935
- 13 Oct 2007, 22:31
- Forum: ✎✎ Lycée
- Sujet: valeur intermédiaire
- Réponses: 7
- Vues: 935
- 13 Oct 2007, 22:06
- Forum: ✎✎ Lycée
- Sujet: valeur intermédiaire
- Réponses: 7
- Vues: 935
valeur intermédiaire
Bonsoir :we:
SVP Aidez-moi à la résolution de cet exo:
Il faut démontrer que :
Quelque soit n de N , cette fonction cosx+cos2x+...+cosnx=0 admet le min une solution à [0;pi].
SVP Aidez-moi à la résolution de cet exo:
Il faut démontrer que :
Quelque soit n de N , cette fonction cosx+cos2x+...+cosnx=0 admet le min une solution à [0;pi].
- 13 Oct 2007, 21:52
- Forum: ✎✎ Lycée
- Sujet: valeur intermédiaire
- Réponses: 7
- Vues: 935
- 32 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :