Forum de Mathématiques: Maths-Forum

J'ai eu des indications par mon prof de maths, merci de votre aide.

Oui

La taille de A n'est-elle pas égale à sa dimension ?

Les conditions pour que A soit diagonalisable sont :
-que la dim(A) soit égale au nombre de racine
-que sur la diagonale de D, on retrouve les racines avec des 0 autour

Je recherche les racines pour pouvoir trouver les vecteurs propres de A puis exprimer P,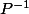 et D tel que D= 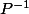AP

Le polynôme a 2 racines distinctes lorsque delta est supérieur à 0, possède une racine confondu lorsque delta est égal à 0 et a des racines complexes quand delta est inférieur à 0. Quand le polynôme possède 2 racines, la matrice est alors diagonalisable ? et que si le polynôme possède en possède qu'...

Bonjour, J'ai calculé les racines (je trouve x1 = a+c et x2 = b-c) cependant quand je remplace X par le x1 puis x2, je ne trouve pas l'équation égale à 0.

Si vous pourriez m'aider !

Merci !

Effectivement (^^") Merci !

Voici l'énoncé : Soient a,b,c des nombres r´eels quelconques. Montrer que la matrice A est diagonalisable.

Bonjour tout le monde ! J'ai un exercice à rendre sur la diagonalisation d'une matrice 2x2. On me demande de montrer que : A: \begin{pmatrix} a & c \\ c & b \end{pmatrix} est diagonalisable. Je commence par modifier la matrice : A= \begin{pmatrix} a-X &c \\ c & b-X \end{pmatrix} Aprè...

d'accord merci !

Bonjour tout le monde, J'ai un exercice à rendre mais je bloque sur une question me demandant de trouver E°(DAH/AH 2 ) à partir des données. Voici mes données: 1. DAH + e^{-} = A^{-} 2. AH 2 = A^{-} + 2 H^{+} + e^{-} E° 1 = -0.16V E° 2 = 0.96V Merci de votre réponse !

D'accord merci !

Oui c'est bien ça ^^"

J'ai recopié mot pour mot mon énoncé et Uk est exprimé par la matrice ...

J'ai fait la question 1 mais je bloque sur la 2.

Bonjour tout le monde, J'ai un DM à rendre pour bientôt mais je suis complètement bloquée... si vous pouvez m'aider ça serait super ! Voici l'énoncé: Soient U o et U 1 des nombres réels. On définit la suite (Un))n∈IN par la donnée de Uo et U1 et de la relation de récurrence : U k+2 = (1 + a)U k+1 −aU...