Forum de Mathématiques: Maths-Forum

Montrer l’a périodicité ?

Bonjour
Je cherche à montrer que c’est periodique mais je ne sait pas comment faire

Bonjour
Comment on montre que c’est periodique
Comment on Montrer que f =(1\2^n).sin(x2^n) est périodique

Bonjour
Montrer que f somme (1\2^n).sin(x2^n)
Je ne vois pas comment on doit faire

Pour tout n ∈ N, on définit fn : R → R par fn(x) = (1/2n)* sin(2nx).
Comment fait-on pour montrer que la somme de fn converge uniformément sur R. On note F sa somme.

bonjour

Bonjour
14)Prendre = est une mauvaise idée puisque on trouve que la machine est bien réglée alors que ce que l on voulait c’est Détecter le dysfonctionnelle de la machine

Bonjour
[]
[0.26,0.826]

Bonjour
[]

Bonjour
Dans l’énoncé on a «Dans toute la suite, on suppose que σ = σ0 »

Bonjour
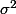=16(40048.79-(200.12)^2/15

Bonjour
J’ai un doute au niveau de intervalle de confiance pour m
[ ,]
Le qu’il faut prendre c’est = ou =

Bonjour
m=200.12 et σ ^2=0,827

Bonjour
J’ai un doute au niveau de intervalle de confiance pour m

Bonjour
Donner une estimation de σ ^2 c’est bien égal à Sn^2?

Je pense que j ai faux je car si σ = σ0 alors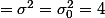
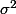
Je trouve 4 n’appartient pas à l’intervalle de confiance de

14. Que pensez-vous de l’hypothèse σ = σ0 ?
Lorsque σ = σ0 on a que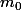 appartient à l’intervalle de confiance de m
Donc la machine est bien réglée

Bonjour
différence entre un intervalle de confiance et un intervalle de confiance bilatéral
Il n’y a pas de différence

Bonjour
Je n’ai pas cette information sur le cours dans le cours on nous montre comment calculer intervalle de confiance dans le cas gaussien espérance connue ,espérance inconnue... mais il n’y a rien de plus

Bonjour
Pour dire qu’une machine est réglée il faut juste montre que m0 appartient pas à intervalle de confiance de m?