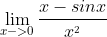6 résultats trouvés
Revenir à la recherche avancée
Re: Bloqué dans le calcul d'une limite.
Bonjour, Supposons x > 0 et posons g(x) = x - sin(x) + x³ g'(x) = 1 - cos(x) + 3x² forcément > 0 --> g est croissante g(0) = 0 ---> x - sin(x) + x³ > 0 (pour x > 0) En divisant par x² > 0, il vient : (x - sin(x))/x² + x > 0 -x <= (x - sin(x))/x² (1) h(x) = x - sin(x) - x³ h'(x) = 1 - cos(x) - 3x² h...
- 09 Oct 2021, 11:52
- Forum: ✎✎ Lycée
- Sujet: Bloqué dans le calcul d'une limite.
- Réponses: 6
- Vues: 527
Re: Bloqué dans le calcul d'une limite.
Alors, pour L'Hopital, ça n' pas été accepté par le prof car on ne l'a jamais fait en cours et pour le développement limité non plus.
Je suis vraiment coincé.
Je suis vraiment coincé.
- 08 Oct 2021, 18:34
- Forum: ✎✎ Lycée
- Sujet: Bloqué dans le calcul d'une limite.
- Réponses: 6
- Vues: 527
- 08 Oct 2021, 14:58
- Forum: ✎✎ Lycée
- Sujet: Bloqué dans le calcul d'une limite.
- Réponses: 6
- Vues: 527
Re: Problème équation
X = x ou X = -x ??
- 12 Jan 2020, 19:27
- Forum: ✎✎ Lycée
- Sujet: Problème équation
- Réponses: 5
- Vues: 330
Re: Problème équation
Je ne sais vraiment pas ce que tu veux dire mais on nous a dit de déduire les solutions d'après les solutions de la première equation
- 12 Jan 2020, 16:38
- Forum: ✎✎ Lycée
- Sujet: Problème équation
- Réponses: 5
- Vues: 330
Problème équation
Bonjour à tous et toute. Je me permet de poser une question. J'ai un exercice que je n'arrive pas à résoudre. Donc premièrement on nous dit résoudre l'équation : x 2 + 5x + 4 = 0 Ce que j'ai fait Et puis on nous demande de déduire les solutions des deux équations : x + 5√x + 4 = 0 et x 4 + 5x 2 + 4 ...
- 12 Jan 2020, 15:35
- Forum: ✎✎ Lycée
- Sujet: Problème équation
- Réponses: 5
- Vues: 330
- 6 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :