Forum de Mathématiques: Maths-Forum

tournesol a écrit:les fonctions et sont solutions de (E)
je n'en sais pas plus .

Comment t a obtenu ce resultat

Bonjour, dans cet exercice on me demande de montrer que l’équation différentielle (F) : 4U" + U^(2n+1) - U = 0 admet une solution unique, et ensuite déterminer cette solution. Sachant que dans la question précédente (la c'est bon il suffit de remplacer l'equation (F) par sa solution et on trouv...

Ben314 a écrit:Salut,
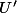
Si tu multiplie l'équation par , ça s'intègrerais pas de façon assez triviale ton truc ?

oui mais je me trouverai face a l' eqt U'^{2} + \frac{U^{2n+2}}{2(n+1)}-\frac{U^{2}}{4}=\frac{C}{2}

Bonjour, dans cet exercice on me demande de montrer que l’équation différentielle (F) : 4U" + U^(2n+1) - U = 0 admet une solution unique, et ensuite déterminer cette solution. Sachant que dans la question précédente (la c'est bon il suffit de remplacer l'equation (F) par sa solution et on trouv...