Forum de Mathématiques: Maths-Forum

Là c’est peut-être possible de chercher
?
Tel que [tex]V_{n+1} = V_n^{2}
Que l’on sait résoudre ?

Ah ok donc c’est bien difficile ! C’est comme
Un² + 1 = Un+1
??

Donc c’est impossible pour ce genre de suite d’avoir une forme explicite exact ?

Ouh c’est intéressant le TAF, faut que je l’apprenne!
Ducoup sa nous donne pas de forme explicite ça nous donne seulement une suite tres proches de Un ?

Fin la limite est très utile et la decroissance aussi mais comment les utiliser pour avoir la forme explicite.?

Non mais je cherche la forme explicite pas la limite ou autre... y’a une technique pour avoir Un en fonction de n ?

Je comprends pas trop là, la limite est Phi (Nombre d’or)
Décroissante et sur R ok mais qu’est ce qu’on en fait ?

Au final

On peut déjà savoir que la forme explicite doit être décroissante et doit avoir comme limite Phi.
J’ai pense au arithmético geo avec q entre [0;1] + Phi
—-) ça donne des valeurs tres proches mais pas égales
, j’ai pensé à une fonction inverse qui serait égal, mais je trouve rien

Mon but est de trouver la forme explicite, je sais déjà que la limite = \frac{1 + \sqrt{5}}{2} Car la suite est décroissante ! En utilisant un raisonnement par récurrence vue que f(x) est croissante sa conserve l’ordre alors Un+1<Un Mais comment trouver U(n) = .... la forme explicite J’ai pu trouver...

Bonjour je suis bloqué sur une suite que je suis incapable de transformer en fonction de n, voici :


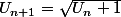
Avec Uo = 3
Et donc j’ai essayé 2 - 3 truc mais rien de convaincant... avez vous des idées ou une solution ? Merci

Bonjour je me demande comment trouver la forme explicite d'une suite tel que,
Un+1 = 1/Un
Merci !

J’avais bien vue la limite avec son parfum de nombre d’or mais je ne vois pas trop quoi en faire là, cette emboîtement de racine me pertube. Merci

Bah en fait c’est moi qui me la suis posé, donc c’est pas guider tu vois mdrr, merci tout de même ! Pas un seul moyen ? Sans conjectures

Bonjour, j’aimerai savoir comment trouver la forme explicite de ce genre de forme :
Un+1 = √(Un + 1) avec Uo = 5
Je ne trouve pas de méthode, comme pour les arithméticogeo ou les autres du style Vn+1 = Vn + 2n -5 Merci