Forum de Mathématiques: Maths-Forum

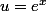
tournesol a écrit:Si l'on ne voit pas cette astuce , sache que les fractions rationnelles en se primitivent facilement en posant car x=ln u et donc

Black Jack a écrit:Salut,

pascal16 a tout dit :


F(x) = 1/(e^x - 1)

en multipliant en haut en bas par exp(-x) ...

F(x) = e^(-x)/[e^(-x).(e^x - 1)]
F(x) = e^(-x)/(1 - e^(-x))

qui, comme pascal16 l'a indiqué est de la forme u'/u

pascal16 a écrit:en multipliant en haut en bas par exp(-x), on a pas une forme u'/u ?

pascal16 a écrit:en multipliant en haut en bas par exp(-x), on a pas une forme u'/u ?

jsvdb a écrit:Okay

jsvdb a écrit:En z tu dois trouver 2 solutions, puis en Z, tu vas en trouver 4 (avec éventuellement des multiplicités)

jsvdb a écrit:Salut GIANNINI.
Pour la première, tu poses et tu commences par résoudre