Forum de Mathématiques: Maths-Forum

Bonjour, J'aurais voulu avoir une justification de l'interprétation en terme de changement de base des opérations élémentaires sur les matrices visant à obtenir une forme dite "échelonnée". Par exemple, si \begin{pmatrix} 6 & 18 \\ 0 & 4\\ 8 & 16 \end{pmatrix} est la matrice d'...

Bah j'imagine que non, vu que l'on doit montrer que l'idéal n'est pas principal... Mais je ne comprends pas la différence avec par exemple l'idéal (2, X) dans \mathbb{C}[X] , qui lui est forcément principal, puisque \mathbb{C}[X] est principal (car euclidien)... Je ne vois pas non plus de po...

Bonjour, Je dois montrer que \mathbb{C}[X,Y] est factoriel mais non principal. Pour le fait qu'il soit factoriel, pas de problème particulier (il suffit de l'écrire sous la forme \mathbb{C}[X][Y] et de dire que l'anneau des polynômes à coefficients dans un anneau factoriel est factoriel). Pour voir ...

Ok, merci !

Bonjour, Je cherche à montrer que l'anneau \mathbb{Z}[i \sqrt{5}] n'est pas factoriel. Pour cela, on introduit N(a+ib \sqrt{5})=a^2+5b^2 , on montre que N(\alpha \beta)=N(\alpha) N(\beta) et que \alpha est inversible dans \mathbb{Z}[i \sqrt{5}] si et seulement si N...

Effectivement, vu comme ça, ça fonctionne. Merci.

Ok, merci.
Mais dans ce cas, comment fais-tu pour montrer Cauchy-Schwarz dans le cas où la forme hermitienne n'est pas supposée définie ?

Bah non, ça marche aussi avec les formes hermitiennes définies positives. Bah c'est pas la même chose "produit scalaire" et "hermitienne définie positive" ? Par ailleurs, tu auras B(x,x) = 0 \Rightarrow x=0 dès lors que par hypothèse \langle Tx,x\rangle = 0 \Rightarrow x...

Bonjour, Dans un cours sur les opérateurs positifs, on a l'inégalité suivante (Cauchy-Schwarz généralisée) : Soit H un espace de Hilbert et T un opérateur positif (i.e. tel que T=T^* et <Tx,x> \; \geq 0, \forall \: x \in H ). \forall \: x,y \: \in H, \: |<Tx,y>| \leq \; <Tx,x>^{1/2} <Ty,y>^{1/2} Pou...

Bonjour, Je cherche à montrer que la convergence en loi n'est pas compatible avec l'addition. Pour cela, j'aimerais trouver trois variables aléatoires X , Y et Z telles que X et Y soient de même loi mais X+Z et Y+Z ne soient pas de même loi. Auriez-vous un exemple simple ? Merci d'avance !

Merci !

Bonjour,

Auriez-vous un exemple d'une suite de variables aléatoires convergeant en probabilités vers une variable aléatoire mais ne convergeant pas dans ?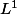

Merci d'avance.