Même avec les cas limite comme tu dis je n'arrive pas à faire sortir le |z|/Re(z) dans l'inégalité...
29 résultats trouvés
Revenir à la recherche avancée
Re: Inégalité sur des complexes
Le cas z imaginaire pure va être compliqué vu que Re(z) > 0 
Même avec les cas limite comme tu dis je n'arrive pas à faire sortir le |z|/Re(z) dans l'inégalité...
Même avec les cas limite comme tu dis je n'arrive pas à faire sortir le |z|/Re(z) dans l'inégalité...
- 21 Jan 2021, 16:11
- Forum: ✯✎ Supérieur
- Sujet: Inégalité sur des complexes
- Réponses: 3
- Vues: 256
Inégalité sur des complexes
Bonsoir, Dans le cadre d'un exercice sur les séries de Dirichlet on me demande de démontrer l'inégalité suivante : Soit z \in \mathbb{C} tel que Re (z) >0 , soient a et b deux réels tels que a<b |e^{-az} - e^{-bz}| \leq \dfrac{|z|}{Re(z)} |e^{-aRe(z)} - e^{-bRe(z)}| E...
- 20 Jan 2021, 23:29
- Forum: ✯✎ Supérieur
- Sujet: Inégalité sur des complexes
- Réponses: 3
- Vues: 256
Un résultat sur des matrices carrés à coefficient entiers
Je vous propose de montrer un petit résultat marrant :
Soit)
On suppose qu'il existe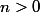 tel que
tel que 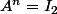
Montrer que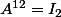
Soit
On suppose qu'il existe
Montrer que
- 19 Nov 2020, 20:48
- Forum: ⚔ Défis et énigmes
- Sujet: Un résultat sur des matrices carrés à coefficient entiers
- Réponses: 0
- Vues: 559
Re: Arithmétique et structures algébriques
Je vais aller zieuter de ce côté ci alors
- 10 Mar 2020, 18:25
- Forum: ✯✎ Supérieur
- Sujet: Arithmétique et structures algébriques
- Réponses: 5
- Vues: 292
Arithmétique et structures algébriques
Bonjour, Je me demandais quels étaient les points communs entre l'anneau Z et l'anneau R[X] qui permettaient de définir sur ses deux anneaux une arithmétique (relation de Bezout, théorème de Gauss). Ma question serait même, quelles sont les conditions minimales sur un ensemble pour pouvoir lui défin...
- 10 Mar 2020, 18:23
- Forum: ✯✎ Supérieur
- Sujet: Arithmétique et structures algébriques
- Réponses: 5
- Vues: 292
Re: Statistiques : Opération sur sommes :
.............................m fois
- 16 Fév 2020, 13:00
- Forum: ✯✎ Supérieur
- Sujet: Statistiques : Opération sur sommes :
- Réponses: 4
- Vues: 393
Re: Statistiques : Opération sur sommes :
Rassembles les deux sommes et multiplies par p(1-p). La lumière devrait se faire voir.
- 16 Fév 2020, 12:12
- Forum: ✯✎ Supérieur
- Sujet: Statistiques : Opération sur sommes :
- Réponses: 4
- Vues: 393
Famille libre polynômiale dans K[X]
Bonjour, j'ai quelques difficultés pour montrer que si A et B sont des polynômes à coefficients constants premiers entre eux et non constants, la famille (A^kB^{n-k})_{0\leq k\leq n} est libre dans K[X]. On montre facilement que si deg(A)\neq deg(B) alors tous les polynômes d...
- 16 Fév 2020, 12:02
- Forum: ✯✎ Supérieur
- Sujet: Famille libre polynômiale dans K[X]
- Réponses: 5
- Vues: 259
Re: essai de DL
Merci beaucoup pour vos réponses!
- 02 Fév 2020, 15:53
- Forum: ✯✎ Supérieur
- Sujet: essai de DL
- Réponses: 3
- Vues: 297
essai de DL
Bonjour, j'essaie d'apprendre les DLs sur le tas. J'aurais aimé savoir si le DL4 suivant était correcte. On cherche le DL4 de sin(x)^{cos(x)} en pi/2 . Pour cela je pose g(h)=sin(pi/2+h)^{cos(pi/2+h)}=cos(h)^{-sin(h)} cos(h) = 1 - h^2/2...
- 02 Fév 2020, 14:26
- Forum: ✯✎ Supérieur
- Sujet: essai de DL
- Réponses: 3
- Vues: 297
Re: Comment écrire en mode mathématiques sur les forums
il faut rajouter les balises "[tex][/ tex]" pour délimiter ton code latex. Ne met pas d'espace entre le / et le tex. Je l'ai rajouté pour que les balises ne soient pas interprétées.
- 01 Fév 2020, 15:00
- Forum: ✯✎ Supérieur
- Sujet: Comment écrire en mode mathématiques sur les forums
- Réponses: 4
- Vues: 349
Re: Intégrale d'un polynôme de Legendre (si je ne m'abuse)
Désolé d'avoir effacé mais c'était trop absurde ce que j'avais répondu (grosse journée on dira)
- 14 Jan 2020, 22:24
- Forum: ✯✎ Supérieur
- Sujet: Intégrale d'un polynôme de Legendre (si je ne m'abuse)
- Réponses: 5
- Vues: 376
Re: Intégrale d'un polynôme de Legendre (si je ne m'abuse)
Oui totalement j'ai écris des bêtises c est pour trouver les valeurs en 1 et -1 de dx)
- 14 Jan 2020, 22:22
- Forum: ✯✎ Supérieur
- Sujet: Intégrale d'un polynôme de Legendre (si je ne m'abuse)
- Réponses: 5
- Vues: 376
Intégrale d'un polynôme de Legendre (si je ne m'abuse)
Bonjour à tous, Je suis tombé par hasard sur cet exercice : Soit L_n=((X^2-1)^n)^(n) * n!/(2n)! Où l'exposant (n) est la dérivée n-ième de (X^2-1)^n 1) Étudier le degré et le coefficient de ce polynôme Pour ça pas de problème 2) Soit Q un polynôme de degré n-1...
- 14 Jan 2020, 22:00
- Forum: ✯✎ Supérieur
- Sujet: Intégrale d'un polynôme de Legendre (si je ne m'abuse)
- Réponses: 5
- Vues: 376
Re: Construction géométrique
Les angles ACM' et MCA sont les mêmes à 2π près d'où la symétrie ! Parfait merci beaucoup pour ta patience !
- 21 Oct 2019, 22:23
- Forum: ✯✎ Supérieur
- Sujet: Construction géométrique
- Réponses: 9
- Vues: 490
Re: Construction géométrique
Honnêtement non la géométrie et moi ça a jamais été une grande histoire d'amour... En fait j'avoue ne plus me souvenir de la caractérisation d'une symétrie axiale. Surtout qu'on ne fait que les similitudes directes en mpsi...
- 21 Oct 2019, 18:10
- Forum: ✯✎ Supérieur
- Sujet: Construction géométrique
- Réponses: 9
- Vues: 490
Re: Construction géométrique
(1) \Leftrightarrow (m' - \frac{a+b}{2})(m-\frac{a+b}{2})=(\frac{a-b}{2})^2 \Leftrightarrow (m'-a+m'-b)(m-a+m-b)=(a-b)^2 Et \frac{m'-a}{m'-b} + \frac{m-a}{m-b} = \frac{(m'-a)(m-b)+(m-a)(m'...
- 21 Oct 2019, 17:45
- Forum: ✯✎ Supérieur
- Sujet: Construction géométrique
- Réponses: 9
- Vues: 490
Re: Construction géométrique
J'aboutit à (m'-a)(m-a)+(m'-b)(m-b)=(a-b)^2 (J'étais déjà allé m'égarer de ce côté ci) mais je ne vois toujours pas la symétrie se montrer... J'ai triché en traçant sur géogebra donc j'in conjecturer que la symétrie se fait par apport à (AB) mais là je...
- 21 Oct 2019, 17:24
- Forum: ✯✎ Supérieur
- Sujet: Construction géométrique
- Réponses: 9
- Vues: 490
Construction géométrique
Le but de l'exercice est d'étudier la construction d'un point M'(m'), tel que: \frac{m'-a}{m'-b}+ \frac{m-a}{m-b} = 0 Après avoir prouvé que A B M et M' étaient cocyclique, on nous demande de prouver (m'-c)(m-c) = (\frac{a-b}{2})^2 (1) avec C(c) le milieu ...
- 21 Oct 2019, 16:06
- Forum: ✯✎ Supérieur
- Sujet: Construction géométrique
- Réponses: 9
- Vues: 490
Re: Application de R dans Q
Je dirais constante. Sinon elle passe forcément par des irrationnels... Il faut donc que f1 soit factorisable par x avec x(rationnel) en haut et en bas ?
- 15 Oct 2019, 12:55
- Forum: ✯✎ Supérieur
- Sujet: Application de R dans Q
- Réponses: 4
- Vues: 256
- 29 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
