19 résultats trouvés
Revenir à la recherche avancée
Re: Groupe symétrique
Non mais ça d'accord ! C'est l'écriture sous forme de produit avec indice qui me pose problème. Tu écris: (i, i+1) (i+1, i+2) (i+2, i+3) (i+1, i+2) (i, i+1) . On voit bien qu'il y a une "régression" qui a lieu au bout d'un moment. Je l'ai indiquée en gras. C'est ça que je n'arrive pas à éc...
- 22 Oct 2020, 20:19
- Forum: ✯✎ Supérieur
- Sujet: Groupe symétrique
- Réponses: 11
- Vues: 564
Re: Groupe symétrique
Oui, j'ai bien réalisé cela.
Je vais prendre un exemple. Soit A appartenant à Sn. On peut écrire A comme le produit allant de j = 1 à m de (ij+1; ij) par le produit allant de j = m-1 à 1 de (ij, ij-1), non ? Je me perds dans ces indices...
Je vais prendre un exemple. Soit A appartenant à Sn. On peut écrire A comme le produit allant de j = 1 à m de (ij+1; ij) par le produit allant de j = m-1 à 1 de (ij, ij-1), non ? Je me perds dans ces indices...
- 22 Oct 2020, 16:32
- Forum: ✯✎ Supérieur
- Sujet: Groupe symétrique
- Réponses: 11
- Vues: 564
Re: Groupe symétrique
Oui, je suis allé trop vite. Oui, dans ce sens là, pas de problème. Mais comment fais-tu pour descendre le valet à la place du 8 ? Comment écris-tu les transpositions dégressives ? C'est justement l'écriture de ce produit (partie ascendante puis partie descendante) qui me pose problème au niveau des...
- 22 Oct 2020, 16:15
- Forum: ✯✎ Supérieur
- Sujet: Groupe symétrique
- Réponses: 11
- Vues: 564
Re: Groupe symétrique
Nous sommes d'accord. J'obtiens l'écriture suivante: (10, V)(9, 10)(8, 9) cela me permet d'avoir l'ordre suivant: 9 10 V 8. Maintenant, je veux déplacer le valet tout à gauche. J'ai donc (V, 9)(10, V). Avec ces deux produits de transpositions élémentaires, j'ai bien échangé le 8 avec le Valet. Mais ...
- 22 Oct 2020, 15:46
- Forum: ✯✎ Supérieur
- Sujet: Groupe symétrique
- Réponses: 11
- Vues: 564
Re: Groupe symétrique
Bonjour, je comprends bien ce que signifie ce théorème. J'arrive à le comprendre sur des exemples mais je n'arrive pas à construire une preuve rigoureuse à partir d'un cas général. Imaginons: soit A un élément de Sn. Je voudrais montrer que A peut s'écrire comme produits de transpositions élémentair...
- 22 Oct 2020, 12:35
- Forum: ✯✎ Supérieur
- Sujet: Groupe symétrique
- Réponses: 11
- Vues: 564
Groupe symétrique
Bonsoir à tous, Je voudrais démontrer rigoureusement ce théorème: tout élément de Sn est égal à un produit de transpositions élémentaires (i, i+1) avec i appartenant à {1, ..., n-1}. Je comprends ce théorème mais je n'arrive à le démontrer de manière rigoureuse. Je me suis aidé d'un exemple. Je suis...
- 20 Oct 2020, 17:31
- Forum: ✯✎ Supérieur
- Sujet: Groupe symétrique
- Réponses: 11
- Vues: 564
Re: Equation différentielle du 1er ordre
Je me suis précipité. Je ne pense pas mettre trompé. En effet, quand on remplace x par \frac{\pi}{2} , on tombe bien sur \frac{\pi}{2} * 1 = \frac{\pi}{2} * 1 car cos(\frac{\pi}{2}) = 0 . Si je prends maintenant le cas général, je trouve que le prolongement par continuité en \frac{\pi}{2} va...
- 29 Juin 2020, 08:38
- Forum: ✯✎ Supérieur
- Sujet: Equation différentielle du 1er ordre
- Réponses: 8
- Vues: 982
Re: Equation différentielle du 1er ordre
Merci pour toute ces explications, elles me sont très utiles. Justement, j'avais commencé à travailler sur un exemple. Je prends le tien, Ben314. Je cherche à savoir si f est prolongeable pour \frac{\Pi}{2} Je calcule la limite quand x tend vers \frac{\Pi}{2} de 3cos(x) +x et je trouve \frac...
- 29 Juin 2020, 07:48
- Forum: ✯✎ Supérieur
- Sujet: Equation différentielle du 1er ordre
- Réponses: 8
- Vues: 982
Re: Equation différentielle du 1er ordre
Merci pour cette aide. Effectivement, c'était évident après observation... Par contre, je suis embêté avec le recollement en pi/2 . J'ai calculé la limite quand x tend vers pi/2 de x + \gamma * cos(x) . Je tombe évidemment sur pi/2. L'idée, c'est de partir sur un prolongement par continuité ...
- 28 Juin 2020, 09:22
- Forum: ✯✎ Supérieur
- Sujet: Equation différentielle du 1er ordre
- Réponses: 8
- Vues: 982
Equation différentielle du 1er ordre
Bonjour à tous, Je cherche à résoudre l'équadiff (E): y'cos(x) + ysin(x) = cos(x) + xsin(x) J'ai commencé par diviser par cos(x) en supposant que cos(x) devait être différent de 0. Je vais donc avoir un point critique à traiter en pi/2 modulo 2pi. (E) devient y...
- 26 Juin 2020, 10:05
- Forum: ✯✎ Supérieur
- Sujet: Equation différentielle du 1er ordre
- Réponses: 8
- Vues: 982
Re: Etude de fonction: tangente hyperbolique
Je voudrais étudier ses variations.
- 22 Mai 2020, 17:13
- Forum: ✯✎ Supérieur
- Sujet: Etude de fonction: tangente hyperbolique
- Réponses: 7
- Vues: 792
Re: Etude de fonction: tangente hyperbolique
Oui, j'ai écrit trop vite. J'ai réécrit th sous forme sh(x)/ch(x) avec x = \frac{x+1}{x-1} J'ai essayé d'encadrer th(\frac{x+1}{x-1}) entre -1 et 1. Mais je n'arrive pas à déterminer la valeur de x. J'ai essayé de passer sous la forme exponentielle avec th(x) mais ça ne donne pas grand chose.
- 22 Mai 2020, 16:54
- Forum: ✯✎ Supérieur
- Sujet: Etude de fonction: tangente hyperbolique
- Réponses: 7
- Vues: 792
Etude de fonction: tangente hyperbolique
Bonjour à tous, Je rencontre une difficulté avec une étude de fonction faisant intervenir une tangente hyperbolique. J'aimerais avoir des indices pour avancer. Je vous soumets la fonction: f(x) = th(\frac{x+1}{x-1}) J'ai écrit th sous la forme f(x) = th(\frac{sh(x)...
- 22 Mai 2020, 14:36
- Forum: ✯✎ Supérieur
- Sujet: Etude de fonction: tangente hyperbolique
- Réponses: 7
- Vues: 792
Re: Démontrer qu'il existe un isomorphisme
Je suis désolé mais je ne vois pas comment tu obtiens cela. Si je prends deux éléments sur (R, *), admettons (a, 0), j'obtiens f(a * 0) = \sqrt[3]{0^3 + a^3} Ca me donne f(a) = a . Je ne comprends pas comment vous obtenez f(a) = a^3 . Pour ce qui est de f^-1(f(a) ...
- 28 Nov 2019, 08:24
- Forum: ✯✎ Supérieur
- Sujet: Démontrer qu'il existe un isomorphisme
- Réponses: 5
- Vues: 416
Re: Démontrer qu'il existe un isomorphisme
Je ne comprends pas d'où tu obtiens ce  = a^3)
Oui, je sais que qu'il faut montrer cette égalité puis la bijection. C'est la démarche qui me pose problème...
Oui, je sais que qu'il faut montrer cette égalité puis la bijection. C'est la démarche qui me pose problème...
- 27 Nov 2019, 22:19
- Forum: ✯✎ Supérieur
- Sujet: Démontrer qu'il existe un isomorphisme
- Réponses: 5
- Vues: 416
Démontrer qu'il existe un isomorphisme
Bonsoir à tous, je rencontre le problème suivant: On munit R de la l.c.i. définie par: a * b = \sqrt[3]{a^3 + b^3} Montrer que (R, *) est isomorphe à (R, +). En déduire que (R, *) est un groupe abélien. Je ne souhaite pas avoir la réponse mais le cheminement qui permet d'atteindre la réponse. J'ai c...
- 27 Nov 2019, 20:06
- Forum: ✯✎ Supérieur
- Sujet: Démontrer qu'il existe un isomorphisme
- Réponses: 5
- Vues: 416
Re: Résolution d'une équation dans C (prépa)
Je ne vois pas où aller avec la factorisation.
Ca me donne:
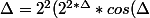^2 - 2^{2*\Delta})
Une coquille ? Je ne crois pas. Où la verrais-tu ?
Ca me donne:
Une coquille ? Je ne crois pas. Où la verrais-tu ?
- 03 Sep 2019, 18:47
- Forum: ✯✎ Supérieur
- Sujet: Résolution d'une équation dans C (prépa)
- Réponses: 6
- Vues: 670
Re: Résolution d'une équation dans C (prépa)
Tu as raison, les formules sont mal écrites. Merci pour l'information, je prends note ! Pour ce qui est du discriminant, voici ce que j'a fait: \Delta = (2^{\Delta +1} * cos(\Delta))^2- 4*2^{2*\Delta} \Delta = 2^{2*\Delta + 2}*cos(\Delta)^2 - 4 *2^{2*\Delta} \Delta = 2^{2*\De...
- 03 Sep 2019, 18:14
- Forum: ✯✎ Supérieur
- Sujet: Résolution d'une équation dans C (prépa)
- Réponses: 6
- Vues: 670
Résolution d'une équation dans C (prépa)
Bonsoir, je suis en train de travailler le chapitre des complexes niveau 1ère année, prépa. Je bute sur l'exercice suivant. J'en appelle à vos lumières. Résoudre dans C l'équation suivante: z^2 - 2^(\Delta + 1)*cos(\Delta)*z + 2^2\Delta = 0 J'ai calculé le discriminant. Je me retrouv...
- 03 Sep 2019, 17:15
- Forum: ✯✎ Supérieur
- Sujet: Résolution d'une équation dans C (prépa)
- Réponses: 6
- Vues: 670
- 19 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
