62 résultats trouvés
Revenir à la recherche avancée
- 20 Mai 2009, 20:56
- Forum: ✯✎ Supérieur
- Sujet: Probabilité + Espérance
- Réponses: 15
- Vues: 1346
Bonsoir,
Oui bien sûr, mathmoica a raison !
La preuve apparaît comme un sophisme presque.
Prendre par exemple gaussienne standard.
gaussienne standard. }{=} -X) donc d'après le théorème qui est faux évidemment, on aurait
donc d'après le théorème qui est faux évidemment, on aurait 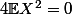 ce qui est faux évidemment.
ce qui est faux évidemment.
Oui bien sûr, mathmoica a raison !
La preuve apparaît comme un sophisme presque.
Prendre par exemple
- 20 Mai 2009, 20:46
- Forum: ✯✎ Supérieur
- Sujet: Probabilité + Espérance
- Réponses: 15
- Vues: 1346
Bonsoir, Sur la physique, je pense que ce n'est pas un mal d'en faire, bien au contraire. En effet, la finance mathématique comporte beaucoup d'équations de physique (exemple : équation de diffusion de la chaleur). Un grand nombre de mathématiciens financiers sont physiciens à la base (exemple : Bla...
- 21 Avr 2009, 21:59
- Forum: ➳ Orientation
- Sujet: Mathématiques financières
- Réponses: 5
- Vues: 6332
Bonsoir,
En termes de débouchés, je pense qu'il est préférable de t'orienter vers Strasbourg, qui propose une filière actuariat de niveau "honorable" (enfin il faut que tu aimes les probabilités et la statistique).
En termes de débouchés, je pense qu'il est préférable de t'orienter vers Strasbourg, qui propose une filière actuariat de niveau "honorable" (enfin il faut que tu aimes les probabilités et la statistique).
- 21 Avr 2009, 21:51
- Forum: ➳ Orientation
- Sujet: Mathématiques... Oui mais ou?
- Réponses: 11
- Vues: 2226
Bonsoir,
L'agrégation interne est beaucoup plus abordable que l'externe. Si tu es motivé, c'est faisable !
L'agrégation interne est beaucoup plus abordable que l'externe. Si tu es motivé, c'est faisable !
- 21 Avr 2009, 21:46
- Forum: ➳ Orientation
- Sujet: Question peut être bête
- Réponses: 8
- Vues: 1368
Bonsoir, Apparemment, il s'agit d'un système de 5 équations à 3 inconnues x,y,z . Le système est donc sur-déterminé. Il n'y a pas de solution. En revanche, il existe une pseudo-solution. On la trouve par la méthode des moindres carrés ordinaires. [Moi aussi je suppose que l'équation est de la forme ...
- 21 Avr 2009, 21:18
- Forum: ✯✎ Supérieur
- Sujet: equation à determiner
- Réponses: 6
- Vues: 857
- 21 Avr 2009, 21:10
- Forum: ✯✎ Supérieur
- Sujet: Mouvement brownien
- Réponses: 3
- Vues: 911
- 19 Avr 2009, 07:34
- Forum: ✯✎ Supérieur
- Sujet: integrale
- Réponses: 4
- Vues: 515
Bonsoir David131,
C'est courageux de reprendre les maths !!
Ton exercice est un problème d'optimisation sous contraintes qui fait appel au lagrangien. Tape ce mot (ou optimisation sous contrainte lagrangien)sous Google, tu auras des références.
Bon courage
C'est courageux de reprendre les maths !!
Ton exercice est un problème d'optimisation sous contraintes qui fait appel au lagrangien. Tape ce mot (ou optimisation sous contrainte lagrangien)sous Google, tu auras des références.
Bon courage
- 18 Avr 2009, 22:53
- Forum: ✯✎ Supérieur
- Sujet: Fonctions quadratiques
- Réponses: 2
- Vues: 545
Bonsoir,
Il me semble qu'il n'est pas utile de passer par la trigo. Un changement de variable de la forme et ensuite une petite intégration par parties qui donne le résultat
et ensuite une petite intégration par parties qui donne le résultat 
Bon courage
Il me semble qu'il n'est pas utile de passer par la trigo. Un changement de variable de la forme
Bon courage
- 18 Avr 2009, 22:44
- Forum: ✯✎ Supérieur
- Sujet: Problème pour la résolution d'une intégrale
- Réponses: 4
- Vues: 1172
Bonsoir, Sauf que, sauf erreur : x^2+2x + 4 = (x+2)^2 Ensuite tu fais la décomposition que tu as citée, sauf qu'il y a une erreur dans ta décomposition : \frac{1}{x(x+2)^2} = \frac{1}{4x} - \frac{1}{2(x+2)^2} - \frac{1}{4(x+2)} Ensuite, c'est simple à intégrer non ? B...
- 18 Avr 2009, 22:37
- Forum: ✯✎ Supérieur
- Sujet: integrale
- Réponses: 4
- Vues: 515
Bonsoir,
Oui ne t'inquiète pas, tu as largement les bagages nécessaires pour faire de la prévision déterministe.
Tu tapes sur google "séries temporelles" tu trouveras ton bonheur.
Bon courage,
Oui ne t'inquiète pas, tu as largement les bagages nécessaires pour faire de la prévision déterministe.
Tu tapes sur google "séries temporelles" tu trouveras ton bonheur.
Bon courage,
- 06 Déc 2008, 21:33
- Forum: ✯✎ Supérieur
- Sujet: méthodes de prévision
- Réponses: 1
- Vues: 898
Bonjour, Oui je pense que c'est plutôt bizarre ! Essayez plutôt cette formule classique : \mathbb{P}\left(\bigcap_{i=1}^k A_i \right) = \mathbb{P} (A_2|A_1) \mathbb{P} (A_3|A_2 \cap A_1) \times ... \times \mathbb{P} (A_k | A_1 \cap ... \cap A_{k-1}) \mathbb{P} (A_...
- 29 Nov 2008, 15:17
- Forum: ✯✎ Supérieur
- Sujet: Variables aléatoires
- Réponses: 9
- Vues: 711
Bonsoir
Calcule la fonction caractéristique d'une uniforme sur [-1,1].
Calcule ensuite la fonction caractéristique de X-Y. Qu'en déduis-tu ?
Calcule la fonction caractéristique d'une uniforme sur [-1,1].
Calcule ensuite la fonction caractéristique de X-Y. Qu'en déduis-tu ?
- 24 Nov 2008, 22:18
- Forum: ✯✎ Supérieur
- Sujet: Proba; variables aléatoires
- Réponses: 1
- Vues: 774
Bonsoir, En fait compte tenu de tes modèles de régression, tu as forcément \bar{y} = \bar{x} + 30 et \bar{x} = 0.25 \bar{y} + 60 Il te reste donc à résoudre le système. Pour trouver la covariance entre X et Y, je pense que tu as besoin d'une hypothèse supplémentaire, par exemple connaitre la varianc...
- 17 Nov 2008, 22:13
- Forum: ✯✎ Supérieur
- Sujet: Statistique simple
- Réponses: 3
- Vues: 1005
Bonsoir,
efyassine a bien intuité le résultat, en tout cas la méthode.
Il suffit d'utiliser le théorème des probabilités totales et la règle de Bayes.
Et ça donne effectivement ça.
efyassine a bien intuité le résultat, en tout cas la méthode.
Il suffit d'utiliser le théorème des probabilités totales et la règle de Bayes.
Et ça donne effectivement ça.
- 09 Nov 2008, 22:34
- Forum: ✯✎ Supérieur
- Sujet: Devoir Probabilité 2eme année
- Réponses: 8
- Vues: 1305
Bonjour,
Tu as un modèle multiplicatif et il te faut un modèle multiplicatif. Quelle fonction permet de linéariser ?
Un indice : Neper est la mathématicien éponyme.
Tu as un modèle multiplicatif et il te faut un modèle multiplicatif. Quelle fonction permet de linéariser ?
Un indice : Neper est la mathématicien éponyme.
- 01 Nov 2008, 22:08
- Forum: ✯✎ Supérieur
- Sujet: Méthode moindres carrés
- Réponses: 1
- Vues: 777
Bonjour,
Sans vouloir être méchant, c'est un problème de terminale. utilise la définition de la probabilité lorsque l'univers est fini :
est fini :
 = \frac{\textrm{card}A}{\textrm{card}\Omega})
Juste un petit indice, ici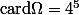
Bon courage
Sans vouloir être méchant, c'est un problème de terminale. utilise la définition de la probabilité lorsque l'univers
Juste un petit indice, ici
Bon courage
- 01 Nov 2008, 21:59
- Forum: ✯✎ Supérieur
- Sujet: Problème probabilités
- Réponses: 2
- Vues: 698
Bonjour,
Tu essaies de montrer que les critères de Cauchy et de d'Alembert conduisent au même résultat. Un petit coup de google et tu auras la solution !
Tu essaies de montrer que les critères de Cauchy et de d'Alembert conduisent au même résultat. Un petit coup de google et tu auras la solution !
- 01 Nov 2008, 21:55
- Forum: ✯✎ Supérieur
- Sujet: convergence d'une suite
- Réponses: 2
- Vues: 777
Bonjour,
Effectivement, ce genre d'équation peut être résolue à l'aide d'une méthode numérique (Newton, gradient conjugué, etc.).
Utilise la fonction Solveur (dans le menu Outils) de excel. Il faut que tu donnes une valeur initiale à a.
Bon courage,
Effectivement, ce genre d'équation peut être résolue à l'aide d'une méthode numérique (Newton, gradient conjugué, etc.).
Utilise la fonction Solveur (dans le menu Outils) de excel. Il faut que tu donnes une valeur initiale à a.
Bon courage,
- 01 Nov 2008, 21:49
- Forum: ✯✎ Supérieur
- Sujet: Risque de Ruine (RoR)
- Réponses: 4
- Vues: 1296
- 62 résultats trouvés - Page 1 sur 4 • 1, 2, 3, 4
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
