Forum de Mathématiques: Maths-Forum

Il convient de montrer que tout élément de B(X, ℇ), ∀ℇ'>0, B(X, ℇ) ∩ B(X, ℇ') ≠ ∅ ce qui est trivial (il existe une distance non nulle entre l'élément et l'enveloppe de la boule). L'adhérence d'une boule ouverte contient les éléments Y qui vérifient d(X - Y) = ℇ puisque pour tout ces Y il existe une...

Adhérence de A : ensemble des X de 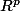qui vérifient : ∀ℇ>0, A ∩ B(X, ℇ) ≠ ∅

L'adhérence pardon

B(X, ε) la boule ouverte centrée en X de rayon ε càd { X de R^p / norme de X < ε }
B_f(X, ε) la boule fermé càd { X de R^p / norme de X ≤ ε }

Bonjour,
"Justifiez que B(X, ε) ⊆ [B(X, ε)]"
N'est ce pas plutôt : B(X, ε) ⊆ [B_f(X, ε)] ?
N'importe quelle boule de rayon positif sur l'enveloppe de la boule ouverte contient des éléments de l'intersection avec celle-ci et fait donc partie de l'adhérence.

Merci ! En effet vrai mais lorsque je l'applique étape par étape j'ai un problème : Avec la méthode du produit en croix : Soit : a / b = c / d a = c / d * b a * d = ( (c / d) * (b) ) * d a * d = ( (c / d) x (b * d) / (1 * d) ) x d a * d = ( ( c + b * d) / ( d ) ) * d a * d = b * d + c Je n'arrive pa...

Revenu de l'étranger après un an, étant en pleine révision pour reprendre une scolarité normale, j'ai des doutes substantielles et récurrent sur des mathématiques basique. Merci d'avance ! Je souhaite simplifier l'équation a/b = c/d, j'ai besoin de l'avoir sous forme a = ...., or si j'ai besoin d'éc...