37 résultats trouvés
Revenir à la recherche avancée
Re: Analyse d'une fonction:
Bonjour. Le sujet est déjà traité ici: https://www.ilemaths.net/sujet-analyse-d-une-fonction-859709.html et ici https://forums.futura-sciences.com/mathematiques-superieur/894604-analyse-dune-fonction.html Par ailleurs, ce n'est pas un sujet du supérieur, c'est un devoir de terminale. https://nosdevo...
- 06 Déc 2020, 12:46
- Forum: ✯✎ Supérieur
- Sujet: Analyse d'une fonction:
- Réponses: 2
- Vues: 485
Re: devoir de maths
Comment démontre-t-on qu'un polynôme du second degré a deux racines ?
- 02 Déc 2020, 18:55
- Forum: ✯✎ Supérieur
- Sujet: devoir de maths
- Réponses: 8
- Vues: 601
Re: devoir de maths
Bonjour, 45K.
D'accord pour t'aider, mais pas pour faire le devoir à ta place.
Donc, il faudrait préciser les questions que tu sais traiter ...
On donnera des indications pour les autres ...
D'accord pour t'aider, mais pas pour faire le devoir à ta place.
Donc, il faudrait préciser les questions que tu sais traiter ...
On donnera des indications pour les autres ...
- 01 Déc 2020, 23:40
- Forum: ✯✎ Supérieur
- Sujet: devoir de maths
- Réponses: 8
- Vues: 601
Re: Calcul d'une limite
Bonjour, Sameraz.
Notons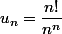 .
.
On peut montrer assez facilement que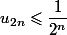 et
et 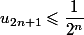 .
.
Notons
On peut montrer assez facilement que
- 01 Déc 2020, 16:21
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'une limite
- Réponses: 1
- Vues: 198
Re: Exercice Maths compliqué
Bonjour, slxavoretro.
Il est normal que tu aies des soucis avec ton exercice, parce qu'il n'a pas de solution.
Pour que soit continue, il faudrait que
soit continue, il faudrait que  (facile à vérifier).
(facile à vérifier).
Mais, si on pose , on peut démontrer que
, on peut démontrer que  n'est pas dérivable en 1.
n'est pas dérivable en 1.
...
Il est normal que tu aies des soucis avec ton exercice, parce qu'il n'a pas de solution.
Pour que
Mais, si on pose
...
- 30 Nov 2020, 19:13
- Forum: ✯✎ Supérieur
- Sujet: Exercice Maths compliqué
- Réponses: 1
- Vues: 262
Re: Polynôme et théorème de Rolle
Non, la rédaction n'est pas correcte. Ici, il ne faut pas partir du résultat qui est demandé (en fait, ce serait possible, mais la rédaction serait tellement plus délicate). Il faut partir du résultat qu'on connaît déjà: il existe c\in ]a,b[ tel que P'(c)=0 . Après, on montre qu'il exist...
- 30 Nov 2020, 02:21
- Forum: ✯✎ Supérieur
- Sujet: Polynôme et théorème de Rolle
- Réponses: 3
- Vues: 289
Re: Inegalité d'une somme
Bonjour, Sameraz . D'abord quelques conseils avant de répondre à ton message: 1) Quand tu demandes une aide, il est conseillé de commencer par une formule de politesse ("bonjour" ...): tes interlocuteurs ne sont pas des robots informatiques. 2) Utiliser tex pour écrire des formules mathéma...
- 29 Nov 2020, 19:32
- Forum: ✯✎ Supérieur
- Sujet: Inegalité d'une somme
- Réponses: 1
- Vues: 234
Re: Polynôme et théorème de Rolle
Bonjour, matt34200 . Il suffit de montrer qu'il existe t\in ]0,1[ tel que c= (1-t)a+tb , et il n'est pas difficile de voir que t=\dfrac{c-a}{b-a} convient. Attention: pour une valeur de c donnée, il correspond une unique valeur de t . Mais il n'y a pas unicité de c et donc pas unicité de t .
- 29 Nov 2020, 00:37
- Forum: ✯✎ Supérieur
- Sujet: Polynôme et théorème de Rolle
- Réponses: 3
- Vues: 289
Re: Dérivabilité
Bonjour, mathelot , GaBuZoMeu et w79exz . J'interviens parce que je pense que la faute commise par w79exz vient d'un sujet précédent https://www.maths-forum.com/superieur/continuite-une-fonction-variables-t227193.html . Dans ce sujet, on arrivait à montrer que la fonction étudiée n'était pas continu...
- 23 Nov 2020, 18:26
- Forum: ✯✎ Supérieur
- Sujet: Dérivabilité
- Réponses: 10
- Vues: 610
Re: Lien intégrale / série
Bonjour, OscarLacoste . Je pense que ce qui suit devrait t'aider. Soit I_{n,p}=\int_0^1 x^n \ln^px \, dx . En intégrant par parties, on a: I_{n,p} = \left[ \dfrac{x^{n+1}}{n+1}\ln^px\right]_0^1 - \dfrac{p}{n+1} \int_0^1 x^n \ln^{p-1} x\, dx =-\dfrac{p}{n+1}I_{n,p-1} Donc, I_{n,n}=\dfrac{(-1)...
- 22 Nov 2020, 22:18
- Forum: ✯✎ Supérieur
- Sujet: Lien intégrale / série
- Réponses: 2
- Vues: 328
Re: DM algèbre L2 maths
Sur la question 3bii: La construction de la base est beaucoup plus simple. (\varphi(e_1),\ldots,\varphi(e_p)) est une famille libre de \ker\varphi , on peut la compléter en une base (\varphi(e_1),\ldots,\varphi(e_p),f_1,\ldots,f_q) de \ker\varphi . Et ...
- 22 Nov 2020, 18:44
- Forum: ✯✎ Supérieur
- Sujet: DM algèbre L2 maths
- Réponses: 14
- Vues: 609
Re: DM algèbre L2 maths
@ ijkl Il y a des endomorphismes qui n'admettent pas de valeur propre (lorsque le corps de base n'est pas algébriquement clos). @ chloe4559 0 est en effet la seule valeur propre de \varphi . Mais tu as écrit dans ta réponse que \varphi pouvait n'avoir aucune valeur propre lorsque \varphi^2=0 . Et ce...
- 22 Nov 2020, 18:29
- Forum: ✯✎ Supérieur
- Sujet: DM algèbre L2 maths
- Réponses: 14
- Vues: 609
Re: DM algèbre L2 maths
Je rappelle que dans la question 2a, il faut montrer que 0 est toujours valeur propre de  .
.
- 22 Nov 2020, 16:06
- Forum: ✯✎ Supérieur
- Sujet: DM algèbre L2 maths
- Réponses: 14
- Vues: 609
Re: DM algèbre L2 maths
Oui. Si e_1,\ldots,e_p sont dans F , alors, \lambda_1e_1+\ldots +\lambda_pe_p est dans F , puisque F est un sous-espace vectoriel. Tu as donc obtenu que \lambda_1e_1+\ldots +\lambda_pe_p est dans F\cap \ker\varphi . Et comme F et \ker\varphi sont en somme directe ... tu n'auras pas de mal à conclure...
- 22 Nov 2020, 15:56
- Forum: ✯✎ Supérieur
- Sujet: DM algèbre L2 maths
- Réponses: 14
- Vues: 609
Re: DM algèbre L2 maths
Bonjour, chloe4559 . Sur la question 2a: Il est exact que si \lambda est une valeur propre de \varphi , alors \lambda = 0 . Mais il faut aussi montrer que 0 est une valeur propre de \varphi . Sur la question 2b: Raisonnement correct, ne pas oublier de préciser que A est la matrice de \varphi dans un...
- 21 Nov 2020, 22:45
- Forum: ✯✎ Supérieur
- Sujet: DM algèbre L2 maths
- Réponses: 14
- Vues: 609
Re: Approximation linéaire
(re)Bonjour, w79exz . En utilisant ta formule, on a: (x_0,y_0)=(3,-2) grad \ f (x_0,y_0)= (\cos(x_0+y_0),\cos(x_0+y_0))=(\cos(1),\cos(1)) L'approximation linéaire de f en (3,-2) est donc: \sin(1)+(x-3)\co...
- 20 Nov 2020, 15:20
- Forum: ✯✎ Supérieur
- Sujet: Approximation linéaire
- Réponses: 3
- Vues: 328
- 20 Nov 2020, 14:55
- Forum: ✯✎ Supérieur
- Sujet: Continuité d'une fonction à 3 variables
- Réponses: 9
- Vues: 645
Re: Continuité d'une fonction à 3 variables
Bonjour, w79exz.
J'ai donné une réponse le 14 novembre, à 0h22.
Qu'en penses-tu ?
J'ai donné une réponse le 14 novembre, à 0h22.
Qu'en penses-tu ?
- 19 Nov 2020, 19:21
- Forum: ✯✎ Supérieur
- Sujet: Continuité d'une fonction à 3 variables
- Réponses: 9
- Vues: 645
Re: Egalité entre partie entière
Bonjour, jonses . Notons p=3\lfloor \sqrt{5}n\rfloor , c'est un entier. On a: \lfloor 3\sqrt{5}n + \sqrt{5} \lfloor \sqrt{5}n\rfloor \rfloor = \lfloor 3\sqrt{5}n + \left( \sqrt{5}-3\right) \lfloor \sqrt{5}n\rfloor +p \rfloor = p + \lfloor 3\sqrt{5}n + \left( \sqrt{5}-3\right) \lfloor...
- 19 Nov 2020, 19:07
- Forum: ✯✎ Supérieur
- Sujet: Egalité entre partie entière
- Réponses: 2
- Vues: 387
- 18 Nov 2020, 19:14
- Forum: ✯✎ Supérieur
- Sujet: Limite avec série de Fourier
- Réponses: 2
- Vues: 324
- 37 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
