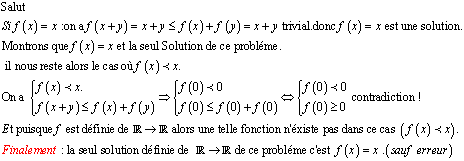Forum de Mathématiques: Maths-Forum

Bonjour,

je n'arrive pas à résoudre l'équation:
2y=x(y'+1/y)+y'^3/3-y'+1
équation de Lagrange
il me faut trouver y la solution

Merci d'avance pour vorte aide




PS : désolé pour l'écriture de l'équation :!:

bonsoir a tous,
pouvez vous m'aider dans cet exercice qui dit:
on définit g:N*-->N* en posant pour n appartient à N*
g(n)=max(ordre p)
p appartient à Sn
determiner g(n) pour n appartient à {1,2,3,4,5,6,7}
merci d'avance

J'aime les mathématiques parce ce que c'est une science précise et profonde. Les mathématiques viennent souvent au secours de d'autres sciences comme les sciences de l'ingénieur et l'économie... Particulièrement, quand il faut étoffer des modèles théoriques où apporter des réponses originales et dét...

et bien, pour x appartient à R+ :|x|<=x est vrai, et comme nous cherchons une solution dans R donc la solution comme vous avez dit f(x)=x
:king2:

bonsoir,
moi personalement j'adore les maths et bien on trouve les maths dans tous les domaines et tu sait quoi les comprendre c'est un art

~oa~ a écrit:

bonsoir à tous,
je crois que ta démonstration est vrai pour f(x)=valeur absolut de x

bonjour, Idée simple de la démo: tu démontres que les nombres de l'ensemble de Cantor sont ceux dont l'écriture décimale en base 3 ne s'écrit qu'avec des 0 ou des 2 (à condition d'admettre les écriture impropres avec une suite infinie de 2 à la fin au lieu de l'écriture "propre": un "1" suivi d'une ...

Bonsoir, pour montrer que les kerfi sont deux à deux distinct selà veut dire qu'il faut que tu trouves que kerf1=/=kerf3 et kerf1=/=kerf4 et kerf3=/=kerf4 alors d'aprés la question (ii) on Fi(idI-fmi)=0 <=> (idI-fmi) appartient au kerfi donc: pour montrer que kerf1=/=kerf3 il suffit de montrer que F...

aussi on me demande aprés de montrer que l'ensemble des fonctions f appartenant a B et continues sur I est sous groupe de (B,+) avec B= l'ensemble des applications de [0,1] dans R j'ai pris deux applications dans B et alors leur difference est aussi dans B donc c'est un sous groupe (avec le fait qu...

bonsoir, Alors pour montrer l'equivalence tu dois montrer l'implication dans les deux sens donc d'abord tu supposes que A est ablien (ie.fg=gf=>f(x).g(x)=g(x).f(x) ) or f(x) et g(x) des elements de G d'ou G est ablien ensuite dans l'autre sens c-à-d tu suppose que G est ablien (ie.a.b=b.a ) or tu pr...

merci pour votre réponse mais moi je veux une définition mathématique avec des equations ou quelque chose de comme ça! vous n'auriez pas une définition mathématique svp.
merci d'avance:-)

Bonsoir tout le mondes,
J’ai un petit problème dans la définition de la géométrie intégrale est ce que vous pouvez me donner la définition détailler de la géométrie intégrale svp ;
Merci d’avance !

busard_des_roseaux a écrit: et ????????????????????

merci à votre réponse mais vous savez sa m'aide pas beaucoup!

bonjour à tous,

Pourriez-vous s'il vous plait me donner la difference entre un polynôme exponentiel et exponentielle-polynôme?
merci d'avance!