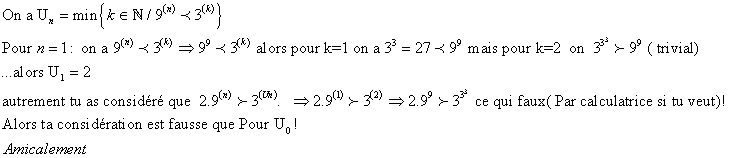40 résultats trouvés
Revenir à la recherche avancée
- 31 Jan 2008, 17:54
- Forum: ✎✎ Lycée
- Sujet: explications
- Réponses: 2
- Vues: 740
Omar a écrit:Et si on dérivait le fonction : f(x)=cos(x)(1+x²)-1 puis démontrer qu'elle est positive quelque soit x appartennant à l'intervalle demandé ?? :hein:
vas y montre nous alors ^^
- 30 Jan 2008, 14:40
- Forum: ⚔ Défis et énigmes
- Sujet: Pas difficile!
- Réponses: 11
- Vues: 1903
Vivica a écrit:C'est bon en dérivant F je tombe sur f
Juste pour être sur: e^x * e^x = e^2x c'est correct ?
Merci de votre aide :we:
Faut révisé tes leçon disant!
- 28 Jan 2008, 21:06
- Forum: ✯✎ Supérieur
- Sujet: Primitive
- Réponses: 12
- Vues: 1114
_-Gaara-_ a écrit:Salut,
c'est des développements limités ? :hein2: Taylor ? :hein:
Je pense que c'est le DL!!
- 28 Jan 2008, 15:29
- Forum: ⚔ Défis et énigmes
- Sujet: Pas difficile!
- Réponses: 11
- Vues: 1903
- 27 Jan 2008, 22:29
- Forum: ⚔ Défis et énigmes
- Sujet: Pas difficile!
- Réponses: 11
- Vues: 1903
Pas difficile!
montrer que cos(x)(1+x²);)1 quelque soit x ]-pi/4,pi/4[
- 26 Jan 2008, 23:42
- Forum: ⚔ Défis et énigmes
- Sujet: Pas difficile!
- Réponses: 11
- Vues: 1903
ThSQ a écrit:Ca me parait pas tout à fait juste. La négation de de f(x)=x pour tout x (sachant que f(x) <= x) c'est pas f(x) < x pour tout x
Salut ThSQ,
désolé mais il ne s'agit pas d'une négation !! c'est une disjonction de cas.
A+
- 26 Jan 2008, 18:15
- Forum: ⚔ Défis et énigmes
- Sujet: olympiade interessant: testez vos capacités
- Réponses: 10
- Vues: 2434
- 14 Jan 2008, 13:00
- Forum: ⚔ Défis et énigmes
- Sujet: olympiade interessant: testez vos capacités
- Réponses: 10
- Vues: 2434
- 10 Jan 2008, 14:19
- Forum: ⚔ Défis et énigmes
- Sujet: olympiade interessant: testez vos capacités
- Réponses: 10
- Vues: 2434
equation type x²+ay²=z² [arithmétique]
SALUT
résoudre dans Z^3 l'équation suivante :
x²+5y²=z²
résoudre dans Z^3 l'équation suivante :
x²+5y²=z²
- 17 Déc 2007, 13:51
- Forum: ⚔ Défis et énigmes
- Sujet: equation type x²+ay²=z² [arithmétique]
- Réponses: 8
- Vues: 1794
lol , j'ai juste remarqué ! mais si on utilise les théorèmes dans nos outils alors pourquoi pas utilisé ceux qui sont plus directe et simple! n'est ce pas raito?
- 16 Déc 2007, 13:13
- Forum: ⚔ Défis et énigmes
- Sujet: Inégalité Difficile.
- Réponses: 22
- Vues: 3688
raito123 a écrit:bonjours,
D'aprés s'être documenter sur , bah un peu!!
Alors sache que Par le réordonnement L'inégalité de tchebychev est démonter !
- 16 Déc 2007, 12:22
- Forum: ⚔ Défis et énigmes
- Sujet: Inégalité Difficile.
- Réponses: 22
- Vues: 3688
raito123 a écrit:salut,
cela revient au même de plus des exo de la sorte demande démontrer un théoreme ou quelque chose donc il ne faut pas faire des applications directes!!!
Ahlan Ayman
C'est évident le théorème de réordonnement pour toi?
- 16 Déc 2007, 12:11
- Forum: ⚔ Défis et énigmes
- Sujet: Inégalité Difficile.
- Réponses: 22
- Vues: 3688
ThSQ a écrit:Y'a rarement une solution unique et ici je vois pas pkoi ta solution est plus simple ou plus "directe".
Bonjour,
Parce que tu as fais une démonstration de l'inégalité de tchebychev a la place de l'appliquée directement!!
- 16 Déc 2007, 11:47
- Forum: ⚔ Défis et énigmes
- Sujet: Inégalité Difficile.
- Réponses: 22
- Vues: 3688
- 16 Déc 2007, 00:38
- Forum: ⚔ Défis et énigmes
- Sujet: Des tours de 9 et de 3
- Réponses: 25
- Vues: 2496
- 40 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :