6102 résultats trouvés
Revenir à la recherche avancée
Re: Calculer
À partir du moment où on l'a sur \mathbb C , on l'a sur tout corps commutatif. En fait, en chassant les dénominateurs, on a une identité polynomiale dans \mathbb Z[X_1,\ldots, X_n] . MMu, ta limite n+1 continue de m'étonner. Ou bien on se limite à la technique élémentaire de la décomposition en élém...
- 01 Fév 2025, 10:43
- Forum: ⚔ Défis et énigmes
- Sujet: Calculer
- Réponses: 8
- Vues: 517
Re: Calculer
Alors, si ce n'est pas une coquille, passons à un cours supérieur d'analyse complexe et traitons le cas où m est un entier quelconque. La décomposition en éléments simples nous dit que \large \dfrac{x_i^m}{\prod_{j\neq i}(x_i-x_j)} est le résidu de la forme différentielle méromorphe \large \...
- 01 Fév 2025, 09:23
- Forum: ⚔ Défis et énigmes
- Sujet: Calculer
- Réponses: 8
- Vues: 517
Re: Calculer
Bonjour, La décomposition en éléments simples de la fraction rationnelle \large \dfrac{X^m}{\prod_{i=1}^n (X-x_i)} = \sum_{i=1}^n \left(\dfrac{x_i^m}{\prod_{j\neq i}(x_i-x_j)}\times \dfrac1{X-x_i}\right) et la technique "multiplier par X , faire tendre X vers l'infini&qu...
- 31 Jan 2025, 10:23
- Forum: ⚔ Défis et énigmes
- Sujet: Calculer
- Réponses: 8
- Vues: 517
Re: Probabilités : convergence presque sûre
Ce n'est visiblement pas encore très clair. La variable aléatoire Z_n , toujours dans la formalisation où \Omega=[0,1]$ muni de la mesure de probabilité de Lebesgue et U : \omega\mapsto \omega , est la fonction Z_n:[0,1]\to \{0,1\} définie par Z_n(\omega)=1 si 0\leq \omega\leq 1/n et Z_n(...
- 30 Jan 2025, 11:52
- Forum: ✯✎ Supérieur
- Sujet: Probabilités : convergence presque sûre
- Réponses: 11
- Vues: 1493
Re: Probabilités : convergence presque sûre
Il reste tout de même pas mal de confusion dans ce que tu écris. Essayons d'y voir plus clair. Tu prends \Omega=[0,1] , c'est un choix raisonnable. Quand je demandais la mesure de probabilité, ce n'était bien sûr pas seulement le fait que la mesure de l'espace complet est 1. Bon, on prend la mesure ...
- 29 Jan 2025, 23:48
- Forum: ✯✎ Supérieur
- Sujet: Probabilités : convergence presque sûre
- Réponses: 11
- Vues: 1493
Re: Probabilités : convergence presque sûre
Non, ça ne va pas du tout. Je crois que tu ne comprends pas la notion de variable aléatoire (je reconnais que ce n'est pas tout simple).
C'est quoi, ton ? C'est quoi, sa mesure de probabilité ? C'est quoi, ta variable aléatoire
? C'est quoi, sa mesure de probabilité ? C'est quoi, ta variable aléatoire  qui a une loi uniforme sur
qui a une loi uniforme sur 
C'est quoi, ton
- 28 Jan 2025, 19:23
- Forum: ✯✎ Supérieur
- Sujet: Probabilités : convergence presque sûre
- Réponses: 11
- Vues: 1493
Re: Probabilités : convergence presque sûre
Merci pour l'ensemble N. Je comprends qu'il est de probabilité nulle pour n infini. Qu'est-ce que ça veut dire ? Il n'y a aucun n qui intervient dans la définition de l'ensemble N . Je répète : N est l'ensemble des \omega\in \Omega tels que U(\omega)=0 . Aucun n là-dedans ! Et ce N\subset \...
- 28 Jan 2025, 14:08
- Forum: ✯✎ Supérieur
- Sujet: Probabilités : convergence presque sûre
- Réponses: 11
- Vues: 1493
Re: Déterminer un triangle équilatéral à partir de 3 cercles
Bonsoir,
Qu'as-tu essayé ?
Qu'as-tu essayé ?
- 27 Jan 2025, 22:13
- Forum: ✯✎ Supérieur
- Sujet: Déterminer un triangle équilatéral à partir de 3 cercles
- Réponses: 10
- Vues: 1687
Re: Probabilités : convergence presque sûre
Bonsoir, Tu as fait une coquille : il faut lire "Posons Z_n=1 pour U inférieur ou égal à 1/n ". Ensuite, Sylvie Méléard t'a donné l'ensemble N : c'est le complémentaire de l'ensemble des \omega \in \Omega tels que U(\omega)>0 , c.-à-d. l'ensemble des \omega tels que U(\omega...
- 25 Jan 2025, 23:29
- Forum: ✯✎ Supérieur
- Sujet: Probabilités : convergence presque sûre
- Réponses: 11
- Vues: 1493
Re: Continuité d'une dérivée partielle
srhmrc a écrit:J'ai ensuite calculé
Ceci ne donne pas la continuité de
Peux-tu expliquer ce que tu as fait avec ton "autre méthode" ?
- 23 Déc 2024, 16:43
- Forum: ✯✎ Supérieur
- Sujet: Continuité d'une dérivée partielle
- Réponses: 6
- Vues: 1036
Re: Continuité d'une dérivée partielle
OK pour la dérivée partielle en (0,0).
As-tu essayé le passage en polaires pour la continuité ? L'argument que tu as donné ne va pas : dans le plan on ne tend pas vers l'origine uniquement suivant l'axe des abscisses !
As-tu essayé le passage en polaires pour la continuité ? L'argument que tu as donné ne va pas : dans le plan on ne tend pas vers l'origine uniquement suivant l'axe des abscisses !
- 23 Déc 2024, 14:32
- Forum: ✯✎ Supérieur
- Sujet: Continuité d'une dérivée partielle
- Réponses: 6
- Vues: 1036
Re: Continuité d'une dérivée partielle
Bonjour,
Pourquoi dis-tu que=0) ?
?
Une méthode possible pour étudier la continuité en) est de passer en coordonnées polaires.
est de passer en coordonnées polaires.
Pourquoi dis-tu que
Une méthode possible pour étudier la continuité en
- 23 Déc 2024, 13:49
- Forum: ✯✎ Supérieur
- Sujet: Continuité d'une dérivée partielle
- Réponses: 6
- Vues: 1036
Re: Parallélogrammes et birapport
Connais-tu le livre "Algèbre géométrique" d'Emil Artin ? J'ai l'impression que ton programme correspond à ce qui est fait dans le deuxième chapitre de ce grand classique.
https://en.wikipedia.org/wiki/Geometric_Algebra_(book)
https://en.wikipedia.org/wiki/Geometric_Algebra_(book)
- 12 Déc 2024, 17:37
- Forum: ⚜ Salon Mathématique
- Sujet: Parallélogrammes et birapport
- Réponses: 7
- Vues: 491
Re: Parallélogrammes et birapport
Bonsoir,
Thalès appliqué plusieurs fois montre que si alors
alors  ,
,
 et
et  . Comme
. Comme 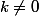 ,
,  .
.
Thalès appliqué plusieurs fois montre que si
- 11 Déc 2024, 20:23
- Forum: ⚜ Salon Mathématique
- Sujet: Parallélogrammes et birapport
- Réponses: 7
- Vues: 491
Re: Problème de suite (sauvez moi mdr)
Ce n'est pas ce qu'écrit Helo0809 : " j'ai montré que la partie entière de a_n était une suite croissante "
- 11 Déc 2024, 20:08
- Forum: ✯✎ Supérieur
- Sujet: Problème de suite (sauvez moi mdr)
- Réponses: 4
- Vues: 1189
Re: Problème de suite (sauvez moi mdr)
Bonsoir,
J'ai compris . Sinon, le problème ne présente effectivement pas grand intérêt.
. Sinon, le problème ne présente effectivement pas grand intérêt.
J'ai compris
- 10 Déc 2024, 21:32
- Forum: ✯✎ Supérieur
- Sujet: Problème de suite (sauvez moi mdr)
- Réponses: 4
- Vues: 1189
Re: Problème forme quadratique
Bonjour, Un petit bémol à ce qu'écrit catamat : on emploie parfois le terme "diagonalisation" au sujet d'une forme quadratique quand il s'agit de trouver une base dans laquelle la matrice de cette forme quadratique est diagonale. Ça revient à la décomposition en carrés de Gauss, et sous fo...
- 09 Déc 2024, 15:24
- Forum: ✯✎ Supérieur
- Sujet: Problème forme quadratique
- Réponses: 5
- Vues: 957
Re: Problème forme quadratique
Bonsoir, Il s'agit de décomposer la partie quadratique de l'équation en carrés (décomposition de Gauss). Grand classique: v_1v_2 = \left(\dfrac{v_1+v_2}2\right)^2- \left(\dfrac{v_1-v_2}2\right)^2 . On peut prendre des nouvelles coordonnées \left\{\begin{aligned}w_1&=\frac12(v...
- 04 Déc 2024, 18:52
- Forum: ✯✎ Supérieur
- Sujet: Problème forme quadratique
- Réponses: 5
- Vues: 957
Re: Longueur de courbe d'une equation à 2 paramètres
Bonsoir,
Pourrais-tu décrire plus précisément la façon dont bouge ton ellipse ? Ton X_0et Y_0dépendent de phi n'est pas très explicite. Ça pourrait peut-être donner une idée d'un autre calcul de l'enveloppe.
Merci.
vam edit
Pourrais-tu décrire plus précisément la façon dont bouge ton ellipse ? Ton X_0et Y_0dépendent de phi n'est pas très explicite. Ça pourrait peut-être donner une idée d'un autre calcul de l'enveloppe.
Merci.
vam edit
- 04 Nov 2024, 21:11
- Forum: ⚜ Salon Mathématique
- Sujet: Longueur de courbe d'une equation à 2 paramètres
- Réponses: 5
- Vues: 426
Re: Cercle inscrit dans un cercle circonscrit
Bonjour,
Plus la corde est grande, et plus la flèche est grande, et la flèche est le diamètre du plus grand cercle contenu dans l'espace entre la corde et l'arc.
Plus la corde est grande, et plus la flèche est grande, et la flèche est le diamètre du plus grand cercle contenu dans l'espace entre la corde et l'arc.
- 30 Aoû 2024, 16:34
- Forum: ✎✎ Lycée
- Sujet: Cercle inscrit dans un cercle circonscrit
- Réponses: 14
- Vues: 827
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
