Bonjour,
Ces coups de bol sont plus que rares, puisque presque sûrement les trois points ne sont pas alignés. Oa alors tu as une tolérance ? Mais comment est-elle définie ?
Bref, pas clair ton histoire.
6103 résultats trouvés
Revenir à la recherche avancée
- 31 Jan 2024, 16:32
- Forum: ⚔ Défis et énigmes
- Sujet: loi uniforme
- Réponses: 57
- Vues: 1482
Re: Dérivabilité
Je t'ai déjà répondu sur ilemaths. Pourquoi viens-tu reposter la même question ici ?
- 28 Jan 2024, 16:27
- Forum: ✎✎ Lycée
- Sujet: Dérivabilité
- Réponses: 2
- Vues: 250
Re: Dérivation, applications et dérivées successives
Bonjour, Tout ce qu'on peut dire : 1) Le titre du fil n'a aucun rapport avec la question 2) Les inégalités de la question 5 sont les deux dernières lignes 3) Vu la structure de l'exercice, on peut se douter que les exemples attendus sont à trouver parmi les trois suites définies dans l'énoncé. Mais ...
- 28 Jan 2024, 11:48
- Forum: ✯✎ Supérieur
- Sujet: Dérivation, applications et dérivées successives
- Réponses: 1
- Vues: 279
Re: Problème d’extremum
Bon, Ben a sorti le ^2) . Mais tant qu'à faire, autant le faire directement sur le numérateur de
. Mais tant qu'à faire, autant le faire directement sur le numérateur de  plutôt que de s'embêter avec le
plutôt que de s'embêter avec le  , non ?
, non ?
- 27 Jan 2024, 10:40
- Forum: ✯✎ Supérieur
- Sujet: Problème d’extremum
- Réponses: 6
- Vues: 251
Re: Problème d’extremum
Bonjour,
Perso, j'arrangerais le numérateur en la somme d'un carré d'une fonction affine de et
et  et d'un polynôme du second degré en
et d'un polynôme du second degré en  (le
(le 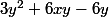 m'y pousse fortement).
m'y pousse fortement).
Perso, j'arrangerais le numérateur en la somme d'un carré d'une fonction affine de
- 27 Jan 2024, 10:21
- Forum: ✯✎ Supérieur
- Sujet: Problème d’extremum
- Réponses: 6
- Vues: 251
Re: Dénombrement
Cette réponse est du n'importe quoi, et elle cache un lien suspect. méfiez-vous !
- 23 Jan 2024, 12:50
- Forum: ⚜ Salon Mathématique
- Sujet: Dénombrement
- Réponses: 13
- Vues: 490
Re: Subjectivité application linéaire, matrice,coeff inconnu
Bonjour,
Tu te trompes de sens.
Le nombre de lignes, c'est la dimension de l'espace d'arrivée et le nombre de colonnes, la dimension de l'espace de départ.
Tu te trompes de sens.
Le nombre de lignes, c'est la dimension de l'espace d'arrivée et le nombre de colonnes, la dimension de l'espace de départ.
- 18 Jan 2024, 13:47
- Forum: ✯✎ Supérieur
- Sujet: Subjectivité application linéaire, matrice,coeff inconnu
- Réponses: 8
- Vues: 946
Re: Extension de corps
Bonjour, Si L et L' sont deux corps extensions du corps K , alors tout K -homomorphisme de L dans L' est un isomorphisme sur son image. Si \sigma est un tel K -homomorphisme et \alpha \in L algébrique sur K de polynôme minimal P , alors \sigma(\alpha) est algébrique sur K de polynôme...
- 12 Jan 2024, 15:55
- Forum: ✯✎ Supérieur
- Sujet: Extension de corps
- Réponses: 1
- Vues: 134
Re: calcul de E(XY) sachant que 3x+y<3
Pas très clair, non.
Pour intégrer sur le triangle de sommets) ,
, ) et
et ) , tu peux intégrer pour
, tu peux intégrer pour  allant de
allant de  à
à ) , puis pour
, puis pour  allant de
allant de  à
à  . Non ?
. Non ?
Pour intégrer sur le triangle de sommets
- 07 Jan 2024, 21:52
- Forum: ✯✎ Supérieur
- Sujet: calcul de E(XY) sachant que 3x+y<3
- Réponses: 4
- Vues: 350
Re: calcul de E(XY) sachant que 3x+y<3
Bonjour, As-tu dessiné le support de la fonction de densité, c'est-à-dire le domaine du plan décrit par les inégalités x>0,\;y>0,\; 3x+y<3 ? Pour t'entraîner à calculer l'espérance de XY , tu peux déjà vérifier que la fonction qu'on te donne est bien une densité de probabilité, en intégrant \frac12&...
- 07 Jan 2024, 21:04
- Forum: ✯✎ Supérieur
- Sujet: calcul de E(XY) sachant que 3x+y<3
- Réponses: 4
- Vues: 350
Re: Similarité de matrices
Comment faire avec la variation de p ? On regarde les dimensions de \ker((A-\lambda I_n)^p) pour p=1,2,3,\ldots en s'arrêtant quand la suite croissante stationne (on a alors atteint le sous-espace caractéristique associé à la valeur propre \lambda ). On peut alors fabriquer une base ...
- 05 Jan 2024, 10:27
- Forum: ✯✎ Supérieur
- Sujet: Similarité de matrices
- Réponses: 5
- Vues: 247
Re: Similarité de matrices
Bonjour, Le sous-espace propre associé à la valeur propre \lambda est \ker(A-\lambda I_n) . L'exemple de Ben314 montre que les dimensions des sous-espaces propres ne suffisent pas. Mais les dimensions des espaces \ker((A-\lambda I_n)^p) où p varie, qui sont aussi invariantes ...
- 04 Jan 2024, 18:06
- Forum: ✯✎ Supérieur
- Sujet: Similarité de matrices
- Réponses: 5
- Vues: 247
Re: dim de GLn(K)
Bonjour et bonne année, Ton titre est "dimension de \mathrm{GL}_n(K) ", et tu précises que K=\mathbb R ou \mathbb C . Si l'on en reste là, la dimension en tant que variété (réelle ou complexe suivant le cas) est n^2 , puisque c'est un ouvert non vide de l'espace vectoriel M_n(K...
- 01 Jan 2024, 10:06
- Forum: ✯✎ Supérieur
- Sujet: dim de GLn(K)
- Réponses: 6
- Vues: 191
Re: P=NP
Bonjour et bonne année,
Tu t'es trompé, on n'est pas le 1er avril !
Tu t'es trompé, on n'est pas le 1er avril !
- 01 Jan 2024, 09:58
- Forum: ✯✎ Supérieur
- Sujet: P=NP
- Réponses: 0
- Vues: 221
Re: 2 a deux distincts
Bonsoir, On te dit que a_1<a_2<\ldots<a_n (inégalités strictes !). Ça force ces n nombres réels à être deux à deux distincts. Que veux-tu dire par "les a_n et les \lambda_n se suivent" ??? On t'a précisé dans l'énoncé que les a_i sont dans l'ordre strictement croissant. On ne dit rien de t...
- 25 Déc 2023, 21:24
- Forum: ✯✎ Supérieur
- Sujet: 2 a deux distincts
- Réponses: 2
- Vues: 564
Re: Variables aléatoires et boules
Bonjour, Combien y a-t-il de tirages en tout ? Ensuite, fixe trois entiers x,y,z tels que n\geq x\geq y\geq z\geq1 . Combien y a-t-il de tirages tels que X=x,\;Y=y,\;Z=z ? Bien sûr, il faut discuter selon que les x,y,z dont distincts, ou s'il y en a deux d'égaux, ou s'il sont tous les trois égaux.
- 20 Déc 2023, 14:02
- Forum: ✯✎ Supérieur
- Sujet: Variables aléatoires et boules
- Réponses: 14
- Vues: 548
Re: Structure algébrique : corps
Pas de bonjour dans le message, pas de sens à la question.
- 17 Déc 2023, 16:39
- Forum: ✯✎ Supérieur
- Sujet: Structure algébrique : corps
- Réponses: 2
- Vues: 189
Re: Interprétation géométrique d'une limite
La dérivée de la dérivée, c'est la dérivée seconde, qui a à voir avec la convexité de la courbe : le signe de la dérivée seconde indique si le graphe de la fonction est au-dessus ou au-dessous de sa tangente.
- 13 Déc 2023, 10:46
- Forum: ⚔ Défis et énigmes
- Sujet: Interprétation géométrique d'une limite
- Réponses: 6
- Vues: 370
Re: Interprétation géométrique d'une limite
Tu n'as pas répondu : qui est  ?
?
- 12 Déc 2023, 17:25
- Forum: ⚔ Défis et énigmes
- Sujet: Interprétation géométrique d'une limite
- Réponses: 6
- Vues: 370
Re: Interprétation géométrique d'une limite
Bonjour,
Cette limite est la dérivée de en
en 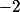 . Qui est
. Qui est  ?
?
Cette limite est la dérivée de
- 12 Déc 2023, 14:20
- Forum: ⚔ Défis et énigmes
- Sujet: Interprétation géométrique d'une limite
- Réponses: 6
- Vues: 370
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
