41 résultats trouvés
Revenir à la recherche avancée
Re: Petite question sur les fonctions différentiable en un p
Merci pour votre réponse tournesol, Dans mon cours, on définit aussi la formule de Taylor à l'ordre 1 : Soient U un ouvert de \mathbb{R}^n et f une fonction de classe C^1 de U dans \mathbb{R}^p . Soit a\in U . Alors, \forall \epsilon, \existe \alpha_\epsilon , \mid \mid h \mid\mid_\infty < \alpha_\e...
- 18 Nov 2019, 23:40
- Forum: ✯✎ Supérieur
- Sujet: Petite question sur les fonctions différentiable en un point
- Réponses: 3
- Vues: 238
Petite question sur les fonctions différentiable en un point
Bonsoir, Je me permets de poser une petit question sur les fonctions différentiables en un point. En effet, On définit les fonctions différentiables comme les fonctions pour lesquelles il existe une matrice Jacobienne Df(a) telle que f(a+h)=f(a)+Df(a)h+o(h) . ...
- 18 Nov 2019, 23:22
- Forum: ✯✎ Supérieur
- Sujet: Petite question sur les fonctions différentiable en un point
- Réponses: 3
- Vues: 238
Re: Devoir Maison Maths
oui,
Ainsi=?)
Ainsi
- 14 Nov 2019, 16:41
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison Maths
- Réponses: 16
- Vues: 728
Re: Devoir Maison STMG
Par exemple,
 alors 3 est la raison
alors 3 est la raison
 alors
alors 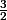 est la raison
est la raison
- 14 Nov 2019, 16:40
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison STMG
- Réponses: 14
- Vues: 1064
Re: Devoir Maison STMG
"Par lui même", je souhaitais plutôt dire "par son terme précédent"
- 14 Nov 2019, 16:38
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison STMG
- Réponses: 14
- Vues: 1064
Re: Devoir Maison STMG
Si on a  alors q est la raison.
alors q est la raison.
Autrement dit, si s'exprime comme un multiple de lui même alors ce multiple est la raison. Or, ce multiples peut-être un réelle.
s'exprime comme un multiple de lui même alors ce multiple est la raison. Or, ce multiples peut-être un réelle.
Autrement dit, si
- 14 Nov 2019, 16:37
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison STMG
- Réponses: 14
- Vues: 1064
Re: Devoir Maison Maths
J'en doute.
Reprenons tranquillement, on a}{(n+1)n}) .
.
Jusqu’à là êtes vous d'accord ?
Si oui alors, développé)
Reprenons tranquillement, on a
Jusqu’à là êtes vous d'accord ?
Si oui alors, développé
- 14 Nov 2019, 16:34
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison Maths
- Réponses: 16
- Vues: 728
Re: Devoir Maison Maths
Malheureusement, vous vous êtes trompé.
En effet, \neq 2n+1)
De même, le dénominateur est\times n)
En effet,
De même, le dénominateur est
- 14 Nov 2019, 16:22
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison Maths
- Réponses: 16
- Vues: 728
Re: Devoir Maison STMG
q est la raison. Par exemple, si  alors 14 est la raison
alors 14 est la raison
- 14 Nov 2019, 16:12
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison STMG
- Réponses: 14
- Vues: 1064
Re: Devoir Maison STMG
Si on souhaite procédé par 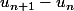 , le plus simple est de remarqué, comme la dit aymanemaysae, que
, le plus simple est de remarqué, comme la dit aymanemaysae, que ) est une suite géométrique. Alors la première question est quel valeur de
est une suite géométrique. Alors la première question est quel valeur de  peut- on trouver avec cette déduction (aymanemaysae la décrite de manière général) ?
peut- on trouver avec cette déduction (aymanemaysae la décrite de manière général) ?
- 14 Nov 2019, 16:06
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison STMG
- Réponses: 14
- Vues: 1064
Re: Devoir Maison Maths
Avec plaisir
- 14 Nov 2019, 14:36
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison Maths
- Réponses: 16
- Vues: 728
Re: Devoir Maison STMG
Bonjour,
Il y a les classiques. Vous pouvez calculer et comparé le résultat par rapport à 1 ou regarder
et comparé le résultat par rapport à 1 ou regarder  et le comparé par rapport à 0.
et le comparé par rapport à 0.
A vous de choisir la meilleur option
Il y a les classiques. Vous pouvez calculer
A vous de choisir la meilleur option
- 14 Nov 2019, 14:36
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison STMG
- Réponses: 14
- Vues: 1064
Re: Devoir Maison Maths
On a 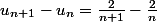 .
.
Souvenez vous,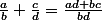
Souvenez vous,
- 14 Nov 2019, 14:31
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison Maths
- Réponses: 16
- Vues: 728
Re: Devoir Maison Maths
Je pense que vous avez fait une erreur de calcul. N'hésitez pas à le refaire.
- 14 Nov 2019, 14:26
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison Maths
- Réponses: 16
- Vues: 728
Re: Devoir Maison Maths
Quel procédé avez vous utilisé ?
Il est peut probable que l'un des deux vous donne 0.
Il est peut probable que l'un des deux vous donne 0.
- 14 Nov 2019, 14:22
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison Maths
- Réponses: 16
- Vues: 728
Re: Devoir Maison Maths
n différent de 0
- 14 Nov 2019, 14:16
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison Maths
- Réponses: 16
- Vues: 728
Re: Devoir Maison Maths
Bonjour,
Si pour tout n entier naturel vn est définie comme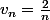
Alors , il y a les classiques. Vous pouvez calculer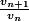 et comparé le résultat par rapport à 1 ou regarder
et comparé le résultat par rapport à 1 ou regarder 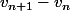 et le comparé par rapport à 0.
et le comparé par rapport à 0.
A vous de choisir la meilleur option
Si pour tout n entier naturel vn est définie comme
Alors , il y a les classiques. Vous pouvez calculer
A vous de choisir la meilleur option
- 14 Nov 2019, 14:15
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison Maths
- Réponses: 16
- Vues: 728
Re: produit scalaire
ah mais oui !
Pardon pour ma bêtise.
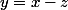
Merci GaBuZoMeu
Pardon pour ma bêtise.
Merci GaBuZoMeu
- 13 Nov 2019, 14:59
- Forum: ✯✎ Supérieur
- Sujet: produit scalaire
- Réponses: 10
- Vues: 313
Re: produit scalaire
y=0 ? autre que cela je ne vois pas
PS : Dans le précédent message, j'ai fais une faute de frappe qui est corrigé maintenant.
PS : Dans le précédent message, j'ai fais une faute de frappe qui est corrigé maintenant.
- 13 Nov 2019, 14:10
- Forum: ✯✎ Supérieur
- Sujet: produit scalaire
- Réponses: 10
- Vues: 313
Re: produit scalaire
oulah,
En effet, mes précédents dire sont atrocement faux.
Donc, pour que il faut et il suffit que
il faut et il suffit que 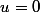
Ainsi, pour que il faut que
il faut que 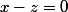 et
et 
D'où légalité entre x et z.
Est ce cela ?
En effet, mes précédents dire sont atrocement faux.
Donc, pour que
Ainsi, pour que
D'où légalité entre x et z.
Est ce cela ?
- 13 Nov 2019, 13:26
- Forum: ✯✎ Supérieur
- Sujet: produit scalaire
- Réponses: 10
- Vues: 313
- 41 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
