Forum de Mathématiques: Maths-Forum

dadou1110 a écrit:quand x tend vers +l'infini 0 et quand il tend vers -l'infini aussi 0 je crois que c'est sa

très bien, je pense que tu as compris le truc :we:
a+

dadou1110 a écrit:d'accord merci beaucoup pour votre aide j'ai bien avancer dans mon devoir au revoir

pas de pb, mais qu'as tu trouvé comme limite alors :hein: ??

Cela veut donc dire qu'il ne faut pas que je m'occupe de e^(-x²) et que regarde seulement la limite en l'infini de e*x c'est ca ? merci d'avance c'est le contraire ! "l'exponentielle l'emporte sur les puissances de x". Donc ce qui compte c'est la limite de l'exponentielle. la valeur de to...

Merci de ta réponse, mais je me suis trompé en postant ma question... :s En fait, c'est lim xexp(-x) = 0 lorsque x tend vers +oo que je ne comprend pas Parce que exp(-x) tend vers 0, mais x tend vers +oo et on tombe sur une forme indéterminée en 0*+oo non ? théorème des croissances comparées... l'e...

dadou1110 a écrit:c'est la première fonction que vous avez mis -e*x*e^(-x²) voila

ok, donc pour ta limite il faut utiliser le théorème des croissances comparées (tu as vu cela en cours je pense) : en résumé l'exponentielle l'emporte toujours sur les puissances de x en +oo et -oo. Ensuite c'est immédiat.

dadou1110 a écrit:Bonjour, pourriez vous m'aidez à trouver la limite en -l'infini et + l'infini de la fonction -ex*e^(-x²) s'il vous plait merci d'avance.

ta fonction c'est quoi au juste : -e*x*e^(-x²)
ou alors -e^(x)*e^(-x²) ??
ce n'est pas clair

dadou1110 a écrit:C'est égal a exp(a+b) c'est sa ? merci d'avance

oui, c'est ça

dadou1110 a écrit:Bonjour, pourriez vous m'aidez à trouver la limite en -l'infini et + l'infini de la fonction -ex*e^(-x²) s'il vous plait merci d'avance.

salut, as-tu pensé à utiliser les formules de base des exponentielles ?? (exp(a)*exp(b) = ...)

fourize a écrit:pour la (a) :
je sais que la courbe est regulier si .

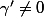
salut
Il faut dire que un point M de la courbe est régulier ssi le couple (;) (0;0)
ça ira mieux je pense...

salut à tout hasard, tu pourrais essayer de trouver une solution évidente. ensuite c'est vrai que ce n'est pas direct pour résoudre l'équation. Donc tu pourrais par exemple montrer que ta fonction est monotone (calcul de dérivée), avec une limite aux bornes de son ensemble de définition (à toi de le...

très bien, juste un truc, au lieu de donner une valeur approchée de R, avec ton équation tu peux dire que R=
a+

salut, à ta place je commencerais par utiliser les formules de bases du style ln(a)+ln(b)= ...
ces formules sont aussi valables pour les "log" car log(x)=ln(x)/ln10

;)-3 ?? aïe aïe....
Le message précédent de Ericovitchi te disait que 2 et -3 sont déjà solutions de ton polynôme -2x³-x²+13x-6.
Donc tu peux en déduire une factorisation de type (x-2)(x+3)(ax+b)

Pour traiter ça je me suis servie du fait que [cos(x)]'=-sin(x) - hello oui, tu as raison, ceci est juste, mais attention, [cos(2x)]' n'est pas égal à -sin(2x)... tu n'as pas "x" dans la parenthèse mais "2x" Regarde dans ton cours la dérivée de cos(U), U étant une fonction de x....

essaye de triturer ce qu'il y a sous la racine carée pour faire apparaitre un truc en au numérateur par exemple...

je t'ai déjà montré
tu as x²0, ça c'est bon je pense (x² toujours positif ou nul)
tu ajoutes 1 de chaque côté de l'inéquation et donc tu as
donc x²+11

donc je peux justifier avec ma phrase ? pour la 3 c'est vrai car si Tout carré est positif ou nul. Si il est nul, alors il y a égalité. S'il est positif alors l'inégalité est stricte donc sachant qu'il y a un moins dvant la fraction elle sera comprise entre -1 et 0 ? oui tu peux utiliser ta phrase,...

tu peux aussi minorer ta suite par une suite divergente connue, exemple très simple : Un= n² Tu connais par exemple la suite de référence Vn=n, qui diverge bien sur tu pourrais dire Un > Vn et Vn diverge, donc Un diverge (bon ici tu peux dire directement que Un diverge, mais c'est pour illustrer...)...

Catro a écrit:comment on montre que l(3;1) est un centre de symétrie de C ?

Un point de coordonnées A(a;b) sera centre de symétrie de ta courbe C ssi f(a+x)+f(a-x)=2*b (tu as du voir cela en cours)

1-Calculer f'(x), f''(x) et f'''(x) Je trouve : f'(x)= http://www.maths-forum.com/images/latex/1b693cc73f4b5fd2103a00046a7d14db.gif f''(x)= http://www.maths-forum.com/images/latex/7aea392edf995f80c5b31459ef993a37.gif f'''(x)= http://www.maths-forum.com/images/latex/5611b93d593dfc686db4c38abd5c75cf....