Forum de Mathématiques: Maths-Forum

Bonsoir a vous je recherche de l'aide sur les automates... J'espere que cela ne derange pas que je poste ici... j'essaye de trouver un automate qui ne contient qu'une seule occurrence de bba avec le langage A={a,b} J'ai essayé par le complementaire et autre, mais je ne trouve pas... Merci pour votre...

Juste pour completer

Si on a 18 = 35 * 468 - 1818 * 9

Et qu'on cherche l'inverse de 196 dans Z/53Z on procede de la meme maniere?

Mais ou est exprimé An?

Tize dans votrepremier post vous m'aviez indiqué que le resultat etait fibo, mais vous avez indiqué



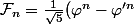Est ce bien

Merci bien a vous

Bonsoir a vous,
Merci pour votre reponse mais je dois avouer ne pas comprendre...

Mon calcule de An est donc faux?

Merci pour votre reponse, il faut donc que je calcule les premiers termes de la suite pour trouver une ressemblance... Donc par exemple, pour celui ci: An+1 = An + A(n-1) + ... + A0 A0 = 1 Les premiers termes sont 1, 1, 2, 4, 8 Donc A(n+1) = 2*An ainsi An = 2^n*A0 Est-ce cela? Pour revenir a l'exemp...

Bonsoir a vous Soit (an) la suite definie par la relation de recurrence A0 = 1 An+1 = An + 2A(n-1) + 3A(n-2) + ... + (n+1) A0 il faut calculer la fonction génératrice A(x) = Somme (An * x^n) pour n>=0 Pour le calcul de la fonction génératrice d'habitude je ne rencontre pas de probleme particulier, m...

Je vous remercie pour vos reponses :we:
oui effectivement on peut le faire de tete :doh:

Bonne soirée a vous

Bonjour a vous tous, Je n'arrive pas a refaire cet exo calculer le reste de 3^(333 333) modulo 11 J'ai eu un autre excercice dans le meme style c'etait 6^(100 000) [Je ne suis pas sur que c'etait les bon chiffres]. Mais il etait plus simple à resoudre, pour decomposer l'exposant, mais la correction ...

Merci pour votre reponse, je pensais que ca allait etre plus complexe :we: ...

Bonne soirée

Bonsoir a vous tous, voila je dois trouver deux entier u et v tels que 473u + 523v = 1 donc: 523 = 473 *1 + 50 473 = 50 * 9 + 23 50 = 23 * 2 + 4 23 = 4 * 5 + 3 4 = 3 * 1 + 1 apres on remonte et on trouve u = -136 et v = 123 mais maintenant on nous demande d'en déduire l'inverse de 473 dans Z/523Z Et...

Bonsoir a vous tous, voila je dois trouver deux entier u et v tels que 473u + 523v = 1 donc: 523 = 473 *1 + 50 473 = 50 * 9 + 23 50 = 23 * 2 + 4 23 = 4 * 5 + 3 4 = 3 * 1 + 1 apres on remonte et on trouve u = -136 et v = 123 mais maintenant on nous demande d'en déduire l'inverse de 473 dans Z/523Z Et...

une petite aide svp :girl2:

Bonsoir a vous tous,
Je ne comprends pas comment on obtient ce resultat, principalement la partie avec le n+1...

(1/(1-2x))^2 = Somme [(2^(i+j)*x^(i+j)}pour i,j >=0 = Somme [(n+1)2^nx^n] pr n>=0

Merci d'avance

Merci a vous tous pour vos reponses !!! :king2:

Je vais adopter la facon de BQss avec passage a la limite :we:

Merci encore

Bonne journée a vous tous

J'avoue ne pas trop comprendre...
N'existe-t-il pas d'autre moyen pour calculer B?
Car la factorisation du second membre fait partie de la decomposition en element simple... alors pourquoi remettre sur le meme denominateur?
Desolé si je fais fausse route lol

Bonjour a vous :we: Voila je ne comprends pas trop comment faire pour obtenir le B dans la formule suivante: (10x^2-63x+29) / [(x-3)(x-4)^2]=A/(x-3) + B/(x-4) +C/(x-4)^2 ps: Pour trouver la formule plus lisible //fr.wikipedia.org/wiki/Fraction_partielle dans le paragraphe sur "Répétition d'un facteu...

Merci beaucoup pour ces explications !!!

Bonne soirée

Merci pour votre aide, j'ai donc trouvé le resultat souhaité.

Mais j'ai une autre question,
dans mon cours sur les series generatrices j'ai :

somme[a^n*x^n] de 0 à n = 1/(1-a*x)

J'avoue ne plus saisir ceci apres avoir vu vos reponses :doh:

Merci encore

Bonsoir a vous, voila je suis confronté a un calcul d'une somme: somme[k*(k-1)*2^k]de k=1 à n en cours nous avons traité les sommes qui pouvaient se reecrire sous la forme du coeff binomial (a+b)^n , avec derivées ou pas... Mais la je ne vois pas trop comment faire pour calculer cette somme... :hum:...

Bonjour a vous tous, voila notre problème; Soit A la matrice 0 1 0 0 0 1 1 0 0 a) M.q. x=1 est l'unique valeur propre réelle de A. Déterminer son sous espace propre associé E 1 Nous avons donc trouvé pour l'unique valeur propre 1 : det (A-xId) = (1-x)(x²+x+1) Mais après on lutte pour trouver le sous...