J'avais commis une erreur de signe et je rectifiais juste.
Merci infiniment pour votre soutien et beaucoup plus pour votre patience GaBuZoMeu
17 résultats trouvés
Revenir à la recherche avancée
- 24 Jan 2020, 23:41
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
Vraiment je suis terrible on a :  et
et  donc en faisant l'application numérique,
donc en faisant l'application numérique,  et je trouve au total
et je trouve au total  à moins que j'ai commis une erreur
à moins que j'ai commis une erreur
- 24 Jan 2020, 21:35
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
Je n'es pas la hauteur H et le demi-angle au sommet du cône pour pouvoir calculer et je ne sais pas si c'est possible de déterminer leurs valeurs
- 24 Jan 2020, 17:46
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
Ah oui j'avais oublié que c'est une partie du dessin qui a été représenté dans le plan XOZ on aura alors S = S1 + 2S2 c'est ça ?
- 24 Jan 2020, 17:16
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
Pour la surface S1 de la partie sphère, on prend r = 1 alors S1 = \int\int\sin\theta d\phi d\theta = 2\pi\sqrt2 Pour la partie cône, nous avons S2 = \int\int r\sin\alpha d\phi dr avec r varie de 0 à rmax et \theta=\alpha demi-angle au sommet du cône de hauteur H après calcul, S2 = \pi\sin\alpha rmax...
- 24 Jan 2020, 16:12
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
J'ai tout fait graphiquement et analytiquement voilà ce que j'ai trouvė
 3
3
- 24 Jan 2020, 12:31
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
Désolé je venais de voir le message.
Oui en mesurant une nouvelle fois l'angle voici ce que j'ai trouvé
voici ce que j'ai trouvé 
Oui en mesurant une nouvelle fois l'angle
- 23 Jan 2020, 20:45
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
Pardon En intégrant le sinus entre 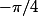 et
et 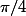 le volume s'annule
le volume s'annule
Si Je comprends bien c'est une coupe du volume et de la surface qui est seulement représentée dans le plan XOZ et on calcul cette surface en prenant # 1 puisqu'on n'est plus sur la surface de la sphère
# 1 puisqu'on n'est plus sur la surface de la sphère
Si Je comprends bien c'est une coupe du volume et de la surface qui est seulement représentée dans le plan XOZ et on calcul cette surface en prenant
- 22 Jan 2020, 00:37
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
Je ne sais pas s'il y'a un problème avec cette intervalle de  parce que le volume s'annule entre
parce que le volume s'annule entre 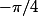 et
et 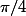 .
.
L'autre surface c'est celle non hachuré et est maintenant différent de 1 je suppose et après on fera la différence des 2 surfaces est-ce celà ?
est maintenant différent de 1 je suppose et après on fera la différence des 2 surfaces est-ce celà ?
L'autre surface c'est celle non hachuré et
- 21 Jan 2020, 22:03
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
Merci pour le dessin

- 21 Jan 2020, 18:23
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
Oui après un petit calcul, j'ai trouvé
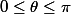
- 21 Jan 2020, 10:59
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Re: Exercice sur calcul le volume et l'aire d'un domaine
1) U en coordonnées sphériques (\rho;\theta;\varphi) 0 ≤ \rho ≤ 1 ; 0 ≤ \theta ≤ \pi /4 0 ≤ \varphi ≤ 2 \pi 2) calcul du volume \int \int \int \rho^2 \sin\theta d\rho d\theta d\varphi = \pi/3(2-\sqrt{2}) 3) s'il vous plaît voici où je suis vraiment coincé sur le calcul d'aire S .
- 21 Jan 2020, 02:42
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Exercice sur calcul le volume et l'aire d'un domaine
Bonsoir, S'il vous plaît, j'ai répondu aux autres questions et je suis bloqué à cette 3eme question On considère dans R^3 le domaine U: {(x, y, z); x^2 + y^2 \geq z^2 ; x^2 + y^2 + z^2 \leq 1 } On note S la surface délimitant U. 1) Décrire U en coordonnées sphériques 2) Calculer le volume de U 3) On...
- 20 Jan 2020, 19:29
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur calcul le volume et l'aire d'un domaine
- Réponses: 33
- Vues: 1194
Arithmétique
Bonsoir, S'il vous plaît je suis bloqué à un niveau. Soit p un entier relatif. On pose a = 4p + 3 et b = 5p +1 En utilisant l'égalité de Bezout, démontrer que a et b sont premiers entre eux. Voici ce que j'ai fait : 5(4p + 3) - 4(5p + 1) = 11 alors que Bezout dit que si au + bv = 1 alors a et b sont...
- 23 Mai 2019, 01:19
- Forum: ✎✎ Lycée
- Sujet: Arithmétique
- Réponses: 2
- Vues: 274
Re: Exercice sur les dénombrements
Ok merci j'ai compris
- 13 Mai 2019, 01:15
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les dénombrements
- Réponses: 4
- Vues: 829
Re: Exercice sur les dénombrements
Ah merci mille fois vous m'avez beaucoup aidé juste une petite explication sur 9999 j'ai essayé de trouver ça en faisant (10^4)-1 mais je ne suis pas sûr
- 11 Mai 2019, 19:52
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les dénombrements
- Réponses: 4
- Vues: 829
Exercice sur les dénombrements
Bonsoir, je suis coincé sur cet exercice. Le service d'immatriculation met à la disposition des automobiles, des plaques de deux modèles comme l'exemple suivant : DD 0001A ou DD 001AA où DD désigne la région d'origine et 0001A ou 001AA le nom d'immatriculation. On rappelle qu'il y a 10 régions au Ca...
- 10 Mai 2019, 18:56
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les dénombrements
- Réponses: 4
- Vues: 829
- 17 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
