51 résultats trouvés
Revenir à la recherche avancée
Re: Lp espace inclusion
Voilà ce que j'ai fais pour démontrer Lp C Lq : On a 1 \leq p \leq q \leq infty Pour x \in L^{p} on a : ||x||^q= \sum_{k}|xk|^q = \sum_{k}|xk|^{q-p}|xk|^p \leq sup_{k}|xk|^{q-p}\sum_{k}|xk|^p \leq [\sum_{k}|xk|^p]^{q-p/p}\sum_{k}|xk|^p =[\sum_{k}|xk|^p]^{q/p} On enlève les racine de chaque cotés et ...
- 17 Jan 2020, 20:14
- Forum: ✯✎ Supérieur
- Sujet: Lp espace inclusion
- Réponses: 10
- Vues: 558
Lp espace inclusion
Bonjour,
Je dois résoudre un exercice qui me demande de montrer que:
Lp[0,1] C Lq[0,1] si 1
Je ne sais pas par où commencer , pourrais je avoir une aide pour le début.
Merci d'avance
Je dois résoudre un exercice qui me demande de montrer que:
Lp[0,1] C Lq[0,1] si 1
Je ne sais pas par où commencer , pourrais je avoir une aide pour le début.
Merci d'avance
- 17 Jan 2020, 14:59
- Forum: ✯✎ Supérieur
- Sujet: Lp espace inclusion
- Réponses: 10
- Vues: 558
Re: Série
D'accord, je vois ce qu'il faut faire merci
- 11 Juin 2019, 15:14
- Forum: ✯✎ Supérieur
- Sujet: Série
- Réponses: 4
- Vues: 229
Série
Bonsoir,
Je bloque sur la nature de la série de terme général:
dn=(1+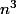 )^1/3-(1+
)^1/3-(1+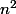 )^1/2
)^1/2
Ma première idée est de faire l'équivalence mais je tombe sur 0
Je bloque sur la nature de la série de terme général:
dn=(1+
Ma première idée est de faire l'équivalence mais je tombe sur 0
- 10 Juin 2019, 18:46
- Forum: ✯✎ Supérieur
- Sujet: Série
- Réponses: 4
- Vues: 229
Re: Valeur d'adhérence
D'accord merci
- 10 Juin 2019, 18:41
- Forum: ✯✎ Supérieur
- Sujet: Valeur d'adhérence
- Réponses: 7
- Vues: 389
Re: Valeur d'adhérence
D'accord mais si j'etudie les sous-suites des termes de rang pair et impair ça marche aussi ?
- 10 Juin 2019, 18:30
- Forum: ✯✎ Supérieur
- Sujet: Valeur d'adhérence
- Réponses: 7
- Vues: 389
Valeur d'adhérence
Bonsoir ,
Je bloque sur le calcul des valeur d'adhérence de la série suivante:
bn=(1-^n}{n}) )^
)^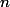
Merci d'avance
Je bloque sur le calcul des valeur d'adhérence de la série suivante:
bn=(1-
Merci d'avance
- 10 Juin 2019, 17:45
- Forum: ✯✎ Supérieur
- Sujet: Valeur d'adhérence
- Réponses: 7
- Vues: 389
Re: Valeur d'adhérence
D'accord j'ai bien compris merci
- 22 Mai 2019, 13:55
- Forum: ✯✎ Supérieur
- Sujet: Valeur d'adhérence
- Réponses: 3
- Vues: 259
Valeur d'adhérence
Bonsoir ,
Je bloque sur un exercice qui est :
On définit la suite (Un)n∈N par la relation de récurrence Un+1 = U^3n pour tout n > 1. Déterminer l’ensemble des valeurs d’adhérence en fonction de U0.
Merci d'avance
Je bloque sur un exercice qui est :
On définit la suite (Un)n∈N par la relation de récurrence Un+1 = U^3n pour tout n > 1. Déterminer l’ensemble des valeurs d’adhérence en fonction de U0.
Merci d'avance
- 21 Mai 2019, 16:44
- Forum: ✯✎ Supérieur
- Sujet: Valeur d'adhérence
- Réponses: 3
- Vues: 259
Re: Produit Scalaire
D'accord merci
- 16 Mai 2019, 12:46
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire
- Réponses: 39
- Vues: 1088
Re: Produit Scalaire
D'accord mais comment j'applique la formule ensuite ?
- 15 Mai 2019, 11:15
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire
- Réponses: 39
- Vues: 1088
Re: Produit Scalaire
D'accord donc si j'applique votre formule je trouve alors :
<(x,y).(1,1)>/||1^2+1^2||.(1,1)
Ce qui me donne
x+y/2.(1,1)
d'où (x+y/2, x+y/2)
<(x,y).(1,1)>/||1^2+1^2||.(1,1)
Ce qui me donne
x+y/2.(1,1)
d'où (x+y/2, x+y/2)
- 15 Mai 2019, 10:08
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire
- Réponses: 39
- Vues: 1088
Re: Produit Scalaire
D'accord merci pour votre aide mais du coup je suis bloquée alors à cette question
- 14 Mai 2019, 21:08
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire
- Réponses: 39
- Vues: 1088
Re: Produit Scalaire
J'ai la base B={(1,0),(1,1)} et u0=(1,1)
donc je fais <e1,u0>/||e1||^2 . e1 + <e2,u0>/||e2||^2 . e2
Je trouve alors
1.(1,0)+1.(1,1)
ce qui me fais (1,0)+(1,1)
Je trouve comme projecteur orthogonale:
Pf(X)=(2,0)
donc je fais <e1,u0>/||e1||^2 . e1 + <e2,u0>/||e2||^2 . e2
Je trouve alors
1.(1,0)+1.(1,1)
ce qui me fais (1,0)+(1,1)
Je trouve comme projecteur orthogonale:
Pf(X)=(2,0)
- 14 Mai 2019, 20:59
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire
- Réponses: 39
- Vues: 1088
Re: forme linéaire/hyperplan
D'accord merci
- 14 Mai 2019, 20:58
- Forum: ✯✎ Supérieur
- Sujet: forme linéaire/hyperplan
- Réponses: 2
- Vues: 315
Re: Produit Scalaire
Oui je l'ai calculé et j'ai trouvé 2
- 14 Mai 2019, 20:37
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire
- Réponses: 39
- Vues: 1088
forme linéaire/hyperplan
Bonsoir ,
Auriez-vous un exemple de forme linéaire et d'hyperplan définie sur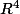
Merci d'avance
Auriez-vous un exemple de forme linéaire et d'hyperplan définie sur
Merci d'avance
- 14 Mai 2019, 20:32
- Forum: ✯✎ Supérieur
- Sujet: forme linéaire/hyperplan
- Réponses: 2
- Vues: 315
Re: Produit Scalaire
Mais maintenant je suis bloquée pour calculer :
d(u,F)= inf||u-v||
d(u,F)= inf||u-v||
- 14 Mai 2019, 19:11
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire
- Réponses: 39
- Vues: 1088
Re: Produit Scalaire
D'accord du coup la base orthogonal est bien B={(1,0),(1,1)} ?
- 14 Mai 2019, 18:58
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire
- Réponses: 39
- Vues: 1088
Re: Produit Scalaire
Non je n'ai pas vus mais du coup j'ai trouvé une autre base qui est :
B={(1,0),(1,1)}
B={(1,0),(1,1)}
- 14 Mai 2019, 17:47
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire
- Réponses: 39
- Vues: 1088
- 51 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
