Bonsoir Benhamedi ,
Vous pouvez utiliser un développement limité à l’ordre 1 de la fonction définie par g(x) = tan(pi/4 + x) = 1 + 2x + o(x)
En utilisant ceci on trouve que le numérateur est égal à o(x) car pleins de choses se simplifient.
25 résultats trouvés
Revenir à la recherche avancée
- 14 Mar 2019, 00:02
- Forum: ✯✎ Supérieur
- Sujet: La limite d'une fonction trigonométrique
- Réponses: 8
- Vues: 514
Re: Arguments/Modules
Soyons fous, je te montre aussi comment faire pour obtenir Z imaginaire pur avec la formule des angles orientés !
https://www.youtube.com/watch?v=miZq7HC ... LZ1HZLwplO
https://www.youtube.com/watch?v=miZq7HC ... LZ1HZLwplO
- 13 Mar 2019, 21:29
- Forum: ✎✎ Lycée
- Sujet: Arguments/Modules
- Réponses: 10
- Vues: 687
Re: Arguments/Modules
Mama27, Chose promise chose due, je t'ai fait une vidéo qui te montre comment obtenir Z réel sans passer par la forme algébrique ni de z ni de Z !! A la place, on utilise la formule des angles orientés : https://www.youtube.com/watch?v=GMm-orsZ-YA&list=PL2hCJKmnwQ2Mym-TqdNTWQ8LZ1HZLwplO Enjoy et...
- 13 Mar 2019, 11:45
- Forum: ✎✎ Lycée
- Sujet: Arguments/Modules
- Réponses: 10
- Vues: 687
Re: Arguments/Modules
Bonjour Mama27, en effet dans cet exemple il existe une autre méthode faisant intervenir la formule arg(zd-zc)/(zb-za) = angle orienté (AB, CD). Mais ceci ne marche que si on a un coeff 1 devant z.
Tout de même je te donnerai une solution détaillée avec la deuxième méthode d'ici demain matin.
Tout de même je te donnerai une solution détaillée avec la deuxième méthode d'ici demain matin.
- 12 Mar 2019, 20:11
- Forum: ✎✎ Lycée
- Sujet: Arguments/Modules
- Réponses: 10
- Vues: 687
Re: Arguments/Modules
Hello Mama27, Je t'ai même fait une vidéo pour voir comment obtenir Z imaginaire pur ! En effet il s'agit ici d’annuler la partie réelle mais c'est un peu délicat à cause du x^2 et y^2... Bon visionnage et dis-moi si ça t'a bien aidé :) https://www.youtube.com/watch?v=icwEN7MRV2A&list=PL2hCJKmnw...
- 11 Mar 2019, 20:22
- Forum: ✎✎ Lycée
- Sujet: Arguments/Modules
- Réponses: 10
- Vues: 687
Re: Arguments/Modules
Bonjour Mama27, Pour savoir à quelle condition Z est un nombre réel on peut dans un premier temps le mettre sous forme algébrique puis trouver z (donc x et y) de sorte à annuler sa partie imaginaire. Je t'ai fait une vidéo complète pour te montrer comment obtenir Z nombre réel !! Enjoy ! https://www...
- 11 Mar 2019, 11:09
- Forum: ✎✎ Lycée
- Sujet: Arguments/Modules
- Réponses: 10
- Vues: 687
Re: DM Maths logarithme népérien
Bonsoir Loulou,
 = (2\frac{\ln\sqrt{x}}{\sqrt{x}})^{2}-\frac{1}{x})
Puis en posant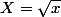 tu te ramènes à une forme du cours
tu te ramènes à une forme du cours }{X}) dont tu connais la limite en plus l'infini (c'est 0)
dont tu connais la limite en plus l'infini (c'est 0)
Puis en posant
- 10 Mar 2019, 00:03
- Forum: ✎✎ Lycée
- Sujet: DM Maths logarithme népérien
- Réponses: 4
- Vues: 529
Re: Dm suite
C'est un plaisir 
Re: Dm suite
Bonsoir SPPalo, je t'ai fait une réponse vidéo détaillée !!
https://www.youtube.com/watch?v=07xuPlInNsc
https://www.youtube.com/watch?v=07xuPlInNsc
Re: Dm suite
Attention $V_{n}=\lambda \alpha^{n}+\mu \beta^{n} $ $V_{n+2}=\lambda \alpha^{n+2}+\mu \beta^{n+2} $ $V_{n+2}=\lambda \alpha^{n}\alpha^{2}+\mu \beta^{n}\beta^{2}} $ $V_{n+2}=\lambda \alpha^{n}(\alpha+1)+\mu \beta^{n}(\beta +1) $ , car alpha et beta sont racines de l'équation x^2 -x-1 ...
Re: Divisibilité et Division euclidienne
La technique de mathelot est très bien !
Cependant la multiplication par 3 membre à membre fait perdre l'équivalence et rend obligatoire la vérification de l'ensemble solution potentiel obtenu.
Cependant la multiplication par 3 membre à membre fait perdre l'équivalence et rend obligatoire la vérification de l'ensemble solution potentiel obtenu.
- 08 Mar 2019, 22:22
- Forum: ✎✎ Lycée
- Sujet: Divisibilité et Division euclidienne
- Réponses: 15
- Vues: 487
Re: Dm suite
Ah oui et pas besoin de remplacer alpha et beta par leurs valeurs exactes, utilise-les tels quels dans les calculs
Re: Dm suite
Bonsoir,
Calcule séparément V(n+2) puis V(n+1)+ V(n) et tu verras que tu obtiens la même expression.
Utilise que alpha et beta sont solutions de l'équation x^2-x-1 = 0
Calcule séparément V(n+2) puis V(n+1)+ V(n) et tu verras que tu obtiens la même expression.
Utilise que alpha et beta sont solutions de l'équation x^2-x-1 = 0
Re: Divisibilité et Division euclidienne
Je pense que la disjonction de cas modulo 7 pour l'entier n est une solution adéquate. En gros on teste n congru à 0 puis 1, 2, 3, 4, 5 et enfin 6 et on regarde ce que ça donne pour la congruence de 41+5n modulo 7 Voici un exemple vidéo : https://www.youtube.com/watch?v=yleFgjdsSsU&list=PL2hCJKm...
- 06 Mar 2019, 23:27
- Forum: ✎✎ Lycée
- Sujet: Divisibilité et Division euclidienne
- Réponses: 15
- Vues: 487
- 02 Mar 2019, 21:03
- Forum: ✎✎ Lycée
- Sujet: Exercices dérivation
- Réponses: 13
- Vues: 1105
Re: les puissances
Shade, Si tu cherches n alors que tu connais l'exposant, tu peux utiliser les racines p-ième
Exemple tu cherches n tel que :
alors
Exemple tu cherches n tel que :
alors
- 02 Mar 2019, 20:42
- Forum: ✎✎ Lycée
- Sujet: les puissances
- Réponses: 11
- Vues: 504
Re: Développement limité
Bonjour,
Un polynôme peut être considéré comme un DL à un ordre arbitrairement grand :
Ici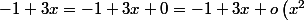 = -1+3x +o\left(x^{1000}\right)) etc.
etc.
Un polynôme peut être considéré comme un DL à un ordre arbitrairement grand :
Ici
- 02 Mar 2019, 10:17
- Forum: ✯✎ Supérieur
- Sujet: Développement limité
- Réponses: 3
- Vues: 278
Re: les puissances
De rien, c'est niveau terminale
- 02 Mar 2019, 10:07
- Forum: ✎✎ Lycée
- Sujet: les puissances
- Réponses: 11
- Vues: 504
Re: les puissances
Bonjour Shade, Ce que tu demandes se ramène à résoudre une équation d'inconnue x : n^{x}=568543 Et si ton inconnue est en exposant tu peux la faire redescendre avec la fonction logarithme népérien. \Leftrightrow \ln(n^{x})=\ln(568543) x\ln(n)=\ln(568543) x=\frac{\ln&#...
- 02 Mar 2019, 09:23
- Forum: ✎✎ Lycée
- Sujet: les puissances
- Réponses: 11
- Vues: 504
Re: Exercices dérivation
Bonjour PhilipeHook, Attention dans l'énoncé il est dit que f est définie sur [0;1] ! Même si l'expression de f permettrait de façon théorique de prendre des valeurs de x autres que celles de l'ensemble de définition [0;1], il n'y a pas le droit de prendre un ensemble de définition plus grand que ce...
- 02 Mar 2019, 09:14
- Forum: ✎✎ Lycée
- Sujet: Exercices dérivation
- Réponses: 13
- Vues: 1105
- 25 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

