Forum de Mathématiques: Maths-Forum

pascal16 a écrit:pour la valuation en 1, tu ne peux pas car car tu fais des division par 0.
tu multiplies de chaque coté par (x-1)²
tu fais x=1
tu as ton E=-9/2 du départ

ok merci beaucoup

Personne ne voit comment faire du coup ?

tournesol a écrit:en faisant x=1 , tu annules des dénominateurs .

merci, j'ai modifié dans la question, mais je tombe toujours sur un système sans solution.

Bonjour, je ne vois pas où est l'erreur dans la décomposition suivante, si vous pouvez m'aider ? f(x)=\frac{x^3-21x-7}{(x^2+1)(x+2)(x-1)^2} Pour faire la décomposition j'ai décomposé comme ca : \frac{Ax+B}{x^2+1}+\frac{C}{x+2}+\frac{D}{x-1}+\frac{E}{(x-1)^2} C...

mathelot a écrit:multiplier par x des deux côtés puis:
faire tendre x vers l'infini
puis
remplacer x par 0
ça donne a=3/4 et b=1/4

Ok je viens de comprendre, merci beaucoup

Carpate a écrit:Décomposition en éléments simples (voir théorie) :

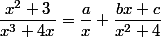
En fait je n'arrive pas à trouver car A=0 et pour trouver B et C il faut passer en nombre complexe d'apres la méthode que je viens de voir.

Carpate a écrit:Décomposition en éléments simples (voir théorie) :

D'accord merci

Bonsoir,

Je suis bloqué sur cette primitive, si vous pouvez m'aider ?



Merci,

ok merci beaucoup pour vos réponses

Kolis a écrit:Je ne vois pas de problème étant donné que est constant sur les intervalles où ne s'annule pas!

Tu penses que ma réponse est correcte ?

Yezu a écrit:Et donc quand on intègre u'/(1+u^2) n'est-ce pas correct ?
Edit : je viens de voir ta modification, je te réponds sou peu, je n'ai pas vraiment lu le fil.

ok merci

en fait je comprends pas comment obtenir le + arctan(1/(sqrt(x²-1))) dans le résultat final

Yezu a écrit:Non, ici tu n'as pas "1/(1+u)" mais plutôt "du/(1+u^2)" ce qui correspond bien à arctan.

J'ai modifié ma question car ce n'était pas tres compréhensible

du n'est pas égale à u', du = u'*dx

arctan u correspond à la primitive de u'/(1+u²) et non 1/(1+u) car ici j'ai un fait un changement de variable !

-

Quand on veut appliquer la décomposition en éléments simples à l'inverse d'un produit de deux facteurs p et q tels que p < q et q - p = a une constante non nulle , alors on calcule la différence 1/p - 1/q qui donne (q - p)/(pq)= a/(pq) ; donc on obtient : 1/(pq) = 1/a (1/p - 1/q) . Pour 1/(t(t² - 2...

Je viens de compléter ma réponse d'en haut : Tu as : \dfrac{1}{t^2-2t}-\dfrac{1}{t^2}=\dfrac{t^2 - t^2 + 2t}{t^2(t^2-2t)} = \dfrac{2t}{t^2(t^2-2t)} = \dfrac{2}{t(t^2-2t)} ; donc tu as : \dfrac{1}{t(t^2-2t)} = \dfrac{1}{2}(\dfrac{1}{t^2-2t} - \dfrac{1}{t^2}) ....

Je viens de compléter ma réponse d'en haut : Tu as : \dfrac{1}{t^2-2t}-\dfrac{1}{t^2}=\dfrac{t^2 - t^2 + 2t}{t^2(t^2-2t)} = \dfrac{2t}{t^2(t^2-2t)} = \dfrac{2}{t(t^2-2t)} ; donc tu as : \dfrac{1}{t(t^2-2t)} = \dfrac{1}{2}(\dfrac{1}{t^2-2t} - \dfrac{1}{t^2}) ....

fibonacci a écrit:bonsoir;

décomposition:

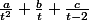
Merci mais je ne vois toujours pas, on obtient encore le même résultat car le à et le b sont égaux à 0 et c=1/2