10 résultats trouvés
Revenir à la recherche avancée
Division euclidienne et nombres complexes
Bonjour, J'essaie de finir cet exercice, mais je bloque à la question suivante : On note \Z[i] l’ensemble des complexes z = a+ib avec a et b appartiennent à \Z . On note N(z) = |z|^2 . [...] 4) Dans cette question, on montre l’existence d’une division euclidienne dans \Z[i] au sens suivant. ...
- 22 Fév 2019, 19:02
- Forum: ✯✎ Supérieur
- Sujet: Nombres complexes inversibles
- Réponses: 4
- Vues: 1193
Re: Nombres complexes inversibles
Si 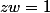 , alors
, alors =1) .
.
DoncN(w) = 1) et donc N(z) = N(w) = 1. D'accord ! (j'en avais déduit que N(z) = 1 / N(w) et je ne voyais pas comment avancer ensuite...)
et donc N(z) = N(w) = 1. D'accord ! (j'en avais déduit que N(z) = 1 / N(w) et je ne voyais pas comment avancer ensuite...)
Donc si N(z) = 1, z = +/-1. ou z = +/- i. C'était tout bête, merci !
Donc
Donc si N(z) = 1, z = +/-1. ou z = +/- i. C'était tout bête, merci !
- 21 Fév 2019, 19:12
- Forum: ✯✎ Supérieur
- Sujet: Nombres complexes inversibles
- Réponses: 4
- Vues: 1193
Nombres complexes inversibles
Bonjour, J'essaie de résoudre cet exercice, mais je bloque à la question 3 : On note Z[i] l’ensemble des complexes z = a+ib. On note N(z) = |z|² = z \overline{z} 1) Montrer que la somme et le produit d’éléments de Z[i] restent dans Z[i]. Soient z = a+ib et w = x+iy deux nombres complexes. z+w = a+x+...
- 21 Fév 2019, 18:54
- Forum: ✯✎ Supérieur
- Sujet: Nombres complexes inversibles
- Réponses: 4
- Vues: 1193
Re: Triangle rectangle et cercle unité
Ah oui, je n'ai pas pensé à remplacer OP par 1. J'avais remplacé les côtés du triangle par leurs valeurs calculées à la question 2 : 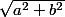 , a et b.
, a et b.
OK, je devrais m'en sortir maintenant, merci encore !
OK, je devrais m'en sortir maintenant, merci encore !
- 11 Fév 2019, 19:26
- Forum: ✯✎ Supérieur
- Sujet: Triangle rectangle et cercle unité
- Réponses: 5
- Vues: 453
Re: Triangle rectangle et cercle unité
Donc si P' est le projeté orthogonal de P sur (OA), on a : \frac{OP}{OC} = \frac{OP'}{OA} = \frac{P'P}{AC} , ce qui fait : \frac{OP}{\sqrt{a^2+b^2}} = \frac{OP'}{a} = \frac{P'P}{b} Comme les longueurs OP' et P'P représentent les coordonnées de P : OP' = \frac{aP'P}{b} P'P = \frac...
- 11 Fév 2019, 19:07
- Forum: ✯✎ Supérieur
- Sujet: Triangle rectangle et cercle unité
- Réponses: 5
- Vues: 453
Triangle rectangle et cercle unité
Bonjour, J'essaye de résoudre cet exercice, mais je bloque à la question 3. 1) Soient (a; b; c) un triplet pythagoricien et notons z = a + ib un nombre complexe. On dira que z engendre un triplet pythagoricien. Quelle est la particularité de z ? On remarque que le module |z|² = a² + b² = c². 2) Noto...
- 11 Fév 2019, 18:23
- Forum: ✯✎ Supérieur
- Sujet: Triangle rectangle et cercle unité
- Réponses: 5
- Vues: 453
Re: Intersection d'une droite et d'un cercle
Ah, oui, je n'étais pas arrivé à simplifier Δ, mais on tombe bien sur un entier au final. Merci beaucoup pour votre aide, je vais m'attaquer à la suite !
- 10 Fév 2019, 12:21
- Forum: ✯✎ Supérieur
- Sujet: Intersection d'une droite et d'un cercle
- Réponses: 9
- Vues: 788
Re: Intersection d'une droite et d'un cercle
Ah, oui je n'ai pas factorisé les bons éléments. Je trouve donc : (1 + t²) x² + (2t²) x + t² - 1 = 0 X1 * X2 = c/a .......... X2 = - c/a .......... X2 = - (t²-1) / (t² + 1) Je pourrais factoriser X2 en - (t - 1)(t+1) / (t + i)(t- i) en utilisant les complexes, mais je ne vois pas trop comment simpli...
- 09 Fév 2019, 20:23
- Forum: ✯✎ Supérieur
- Sujet: Intersection d'une droite et d'un cercle
- Réponses: 9
- Vues: 788
Re: Intersection d'une droite et d'un cercle
Merci, Aviateur. J'ai l'équation : x² + x (t²x + 2t²) + t² - 1 = 0 avec : a = 1 b = (t²x + 2t²) c= t² - 1 Effectivement, les relations entre les racines sont bien pratiques. Donc X1 * X2 = c/a ..................... X2 = - c/a = -t² + 1 En remplaçant X2 dans l'équation de la droite : (Dt) : y = tx + ...
- 09 Fév 2019, 19:44
- Forum: ✯✎ Supérieur
- Sujet: Intersection d'une droite et d'un cercle
- Réponses: 9
- Vues: 788
Intersection d'une droite et d'un cercle
Bonjour tout le monde, Voici l'énoncé d'un exercice que j'essaie de résoudre : 1) Soit Q=(-1, 0). Fixons t un réel et notons T=(0, t ). Déterminer l'équation cartésienne de la droite (Dt) qui passe par Q et T. J'ai procédé ainsi : (Dt) : y = mx + p Les coordonnées de Q vérifient 0 = -m + p , donc p ...
- 09 Fév 2019, 19:05
- Forum: ✯✎ Supérieur
- Sujet: Intersection d'une droite et d'un cercle
- Réponses: 9
- Vues: 788
- 10 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
