275 résultats trouvés
Revenir à la recherche avancée
C'est effectivement possible. Ton exemple est bon. On peut aussi penser à quelque choise d'un peu moins anecdotique : un mouvement brownien partant de 1 que l'on stoppe à zéro dès que l'on passe en négatif. On peut vérifier que c'est encore une matingale.
- 18 Jan 2010, 12:05
- Forum: ✯✎ Supérieur
- Sujet: Martingale strictement positive ?
- Réponses: 2
- Vues: 963
Tu peut noter que si  , alors
, alors }) . En commant, on obtient que
. En commant, on obtient que }) . Or la deuxième somme est une somme téléscopique et vaut 1.
. Or la deuxième somme est une somme téléscopique et vaut 1.
- 17 Jan 2010, 22:11
- Forum: ✯✎ Supérieur
- Sujet: suites
- Réponses: 7
- Vues: 496
Il est quand même utile de se souvenir que le logarithme est une fonction concave, donc inférieure à toutes ses applications tangentes.
- 23 Fév 2009, 17:12
- Forum: ✯✎ Supérieur
- Sujet: Comparaison série - intégrale
- Réponses: 6
- Vues: 1273
Si l'on suppose la série de 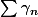 absolument convergente, on s'en tire très facilement par convergence dominée. (Indice : rentrer le
absolument convergente, on s'en tire très facilement par convergence dominée. (Indice : rentrer le 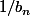 dans la somme)
dans la somme)
Si on en le suppose pas, il faut le faire à la main, mais c'est plus laborieux.
Si on en le suppose pas, il faut le faire à la main, mais c'est plus laborieux.
- 01 Aoû 2008, 16:58
- Forum: ✯✎ Supérieur
- Sujet: Suites et séries réelles
- Réponses: 22
- Vues: 2167
mathelot a écrit:Par exemple
ensemble majoré , sans borne supérieure.
Pas de borne sup rationnelle ! Mais dans
- 17 Juil 2008, 19:37
- Forum: ✯✎ Supérieur
- Sujet: Unicité du supremum d'un intervalle
- Réponses: 11
- Vues: 2421
En probabilités, on suppose des conditions sur une loi (dont la justification n'est pas du ressort des probas mais de celui qui modélise) et on raisonne dessus.
En statistiques, on part d'une série d'expérience et on cherche à décrire la loi.
En statistiques, on part d'une série d'expérience et on cherche à décrire la loi.
- 17 Juil 2008, 18:18
- Forum: ✯✎ Supérieur
- Sujet: Différence Probas Stats
- Réponses: 4
- Vues: 8852
Re-bonjour Bon alors la solution proposé semble marcher. Nous avons donc démontré que si (S,<) est bien ordonné avec S dénombrable alors il existe une injection croissante de S dans R... Bon alors maintenant si on travaille avec les ordinaux et qu'on prend l'ensemble w qui est définit comme le plus...
- 17 Juil 2008, 18:12
- Forum: ✯✎ Supérieur
- Sujet: fonction injective et ensemble bien ordonné
- Réponses: 33
- Vues: 2935
Voici une solution correcte : Soit a : S \to \mathbb{N} une bijection. Une solution du problème proposé est alors donnée par \forall x\in S, f(x) = \sum_{y \leq x} 2^{-a(y)} . Comme S est dénombrable et que (2^{-n})_n est une famille sommable, la somme est toujours finie. Com...
- 14 Juil 2008, 15:24
- Forum: ✯✎ Supérieur
- Sujet: fonction injective et ensemble bien ordonné
- Réponses: 33
- Vues: 2935
- 23 Juin 2008, 23:00
- Forum: ⚔ Défis et énigmes
- Sujet: Arithmétique
- Réponses: 10
- Vues: 1567
- 17 Juin 2008, 19:59
- Forum: ✯✎ Supérieur
- Sujet: Série et fractions rationelles
- Réponses: 10
- Vues: 1117
Sur une table ronde, la notion de place est floue... Il y a une place que si on y met une assiette. Et il est coutume de mettre autant d'assiette que de convive :) Donc... 1. 10!, c'est clair (ou alors relis ton cours). 2. 9!, c'est clair encore. 3. Comme la maitresse de maison est placée, on sait o...
- 17 Juin 2008, 19:46
- Forum: ✯✎ Supérieur
- Sujet: un tit prroblèm' en analyse combinatoire .
- Réponses: 10
- Vues: 2206
- 12 Juin 2008, 17:48
- Forum: ⚜ Salon Mathématique
- Sujet: Défi : Curiosités sur Pi
- Réponses: 24
- Vues: 2908
Si ma mémoire est bonne, on retrouve le même phénomène aux rang 315 et 384. Et en fait, au rang 360, il y a quelque chose de plus fort puisque les décimales à partir du rang 357 sont 0,3,6,0 qui finit au rang 0360. On note de plus que ce phénomène ne se produit pas pour des nombre de 2, 5 ou 6 et qu...
- 11 Juin 2008, 18:01
- Forum: ⚜ Salon Mathématique
- Sujet: Défi : Curiosités sur Pi
- Réponses: 24
- Vues: 2908
- 14 Mai 2008, 11:43
- Forum: ✯✎ Supérieur
- Sujet: probleme sur une Projection Orthogonale
- Réponses: 2
- Vues: 1143
Pour toutes ces histoires de sommes directes, il n'y a qu'une seule chose à savoir : la définition ! Soit (F_i)_{i\in I} , avec I fini ici, une famille de s.e.v de E. On considère l'application linéaire \phi : (x_i)_i\in\prod_{i\in I} F_i \to \sum_i x_i \in E . On définit \sum_{i\in ...
- 14 Mai 2008, 07:10
- Forum: ✯✎ Supérieur
- Sujet: Somme directe
- Réponses: 5
- Vues: 819
- 11 Mai 2008, 22:04
- Forum: ✯✎ Supérieur
- Sujet: Sur la théorie de la mesure...
- Réponses: 9
- Vues: 895
En fait, il n'y a pas besoin de récurrence. On pose \Large A=\( \array{1&1&1\\1&1&1\\1&1&1}\) On a alors M = A - 2I. A^2 = 3A . Donc A^k = 3A^{k-1} = 3^{k-1}A . Or I et A commutent, donc M^n = \sum_{k=0}^n C_{n}^k A^k (-2)^{n-k} I^{n-k} . Ce qui donne M^n = &#...
- 09 Mai 2008, 10:24
- Forum: ✯✎ Supérieur
- Sujet: matrice et récurrence
- Réponses: 4
- Vues: 939
tize a écrit:Plutôt d'accord avec ThSQ, sans un calculateur c'est pas la joie...mais bon y'en a qui aime ça...
Sinon pour le détail du o(1) :
Il faudrait transformer le o(1/n) en O(1/n²) et donner une borne explicite.
- 09 Mai 2008, 10:07
- Forum: ✯✎ Supérieur
- Sujet: Le plus petit
- Réponses: 9
- Vues: 814
Je voulais dire par là que c'était faux ! Donc que tout ce qui suit aussi. Deux endomorphismes diagonaux commutent. Mais deux endomorphismes diagonalisables ne le sont pas nécessairement dans la même base donc ne commutent pas forcément.
- 08 Mai 2008, 18:51
- Forum: ✯✎ Supérieur
- Sujet: Endomorphisme normaux
- Réponses: 9
- Vues: 1307
Salut ThSQ Ce n'est pas une question d'oral, c'est de ma propre imagination. Mais la question reste toujours: est-ce qu'on peut trouver ce n sans l'aide d'un ordinateur?!!! On peut facilement trouver un ordre de grandeur, à savoir e^{10 - .577} . En effet, on a le développement asymptotique \sum_{k...
- 08 Mai 2008, 18:47
- Forum: ✯✎ Supérieur
- Sujet: Le plus petit
- Réponses: 9
- Vues: 814
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
