9 résultats trouvés
Revenir à la recherche avancée
exercice sur les entiers
montrer que ^n((1+\frac{1}{n})<1)
- 17 Aoû 2019, 11:34
- Forum: ✎✎ Lycée
- Sujet: exercice sur les entiers
- Réponses: 1
- Vues: 453
Re: exercice sur l'absurde
j'ai trouvé que 
et que n et n+2 sont impaires
et que n et n+2 sont impaires
- 15 Aoû 2019, 14:43
- Forum: ✎✎ Lycée
- Sujet: exercice sur l'absurde
- Réponses: 3
- Vues: 281
exercice sur l'absurde
Montrer que 
- 15 Aoû 2019, 14:32
- Forum: ✎✎ Lycée
- Sujet: exercice sur l'absurde
- Réponses: 3
- Vues: 281
Re: exercice d'absurde
montrer que 
- 15 Aoû 2019, 13:35
- Forum: ✎✎ Lycée
- Sujet: exercice d'absurde
- Réponses: 3
- Vues: 336
exercice d'absurde
montrer que 
- 15 Aoû 2019, 11:03
- Forum: ✎✎ Lycée
- Sujet: exercice d'absurde
- Réponses: 3
- Vues: 336
Re: exercice sur l'encadrement
c niveau tronc commun
- 17 Fév 2019, 09:55
- Forum: ✎✎ Lycée
- Sujet: exercice sur l'encadrement
- Réponses: 4
- Vues: 351
- 17 Fév 2019, 02:06
- Forum: ✎✎ Lycée
- Sujet: exercice sur l'encadrement
- Réponses: 4
- Vues: 351
exercice sur l'encadrement
soient a et b deux réels tel que:
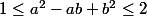
montrer que
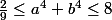
montrer que
- 17 Fév 2019, 01:52
- Forum: ✎✎ Lycée
- Sujet: exercice sur l'encadrement
- Réponses: 4
- Vues: 351
autour de l'inégalité de shapiro. qst 3
Soient a et b et c et d des nombres réels strictement positifs. On pose S=\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b} 1) montrer que \left(a+b+c+d \right)^{2}\geq 4\left( a+b\right)\left(c+d \right) 2) montrer que a^{2}+b^{2}+c^{2}+d^{2}+ad+dc+cb+ba\geq \frac{1}{2...
- 21 Jan 2019, 00:02
- Forum: ✎✎ Lycée
- Sujet: autour de l'inégalité de shapiro. qst 3
- Réponses: 2
- Vues: 374
- 9 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
