Forum de Mathématiques: Maths-Forum

Merci pour vos reponses !

En considérant et en effectuant un developpement limité (asymptotique) à l'ordre 3 et en sommant sur le reste des sommes partielles on obtient le deuxiele terme du DL

Up

parce que P est scindé à racines simples et l'evaluation en 1 donne le resultat avec P=X^n+1

J'ai oublié un moins en cours de route dans le resultat precedent

Ah ouais merci !

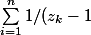=-n/2 parce que ça vaut P est scindé à racines simples

Comment faire apparaitre le dernier terme de l'egalité ?

Edit : il y a un moins devant n/2

Ok j'admets que c'est de degré n, mais comment on en est sur que cela ne marche pas pour les autres polynomes ?



Et après pourquoi (1-X)^2 au dénominateur ?

Edit : la somme part de 1

Bonjour à tous,

Comment trouver un developement asymptotique à 2 termes de la suite verifiant :



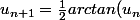NB: je trouve u(n) equivaut à alpha/2^n mais j'arrive pas à trouver le alpha

Bonjour, j'ai pris du temps a repondre j'avais oublié désolé @aviateur : P est un polynome à coefficients complexes de degré quelquonque j'ai oublié de le préciser, je pense que la somme part de 1 dans l'énoncé @GaBuZoMeu : Oui c'est ça la somme part de 1 dans l'enoncé et z0 n'existe pas, je vais éd...

Bonjour à tous, Comment établir : XP'(X)=\frac{n}{2}P(X) + \frac{2}{n} \sum_{k=0}^n \frac{z_kP(z_kX)}{(z_k-1)^2} où les z_k sont les racines de X^n+1 Est-ce que il y a un lien avec les ponynomes de tchebychev ? Edit : la somme part de 1 et P est un polynome a coef...

Ohhhh j'ai compris merci !

Une fois que tAA=S^2, comment on fait pour trouver A=QS avec Q orthogonale ?

Merci pour vos réponses, j'ai compris !

A appartient à Sn+ si tXAX est superieur à 0 pour tout X

Bonsoir à tous,

Soient A appartenant à Mn(R), et c un réel, et I la matrice identité montrer que cI-tAA appartient à Sn+ si et seulement si cI-AtA appartient à Sn+

Quelqu'un a une piste svp ?

Merci pour vos réponses !

Dans la deuxième question, avec quelle valeur évaluer a dans J(a) pour trouver I ?

Bonjour, Soient : J(a)= \[ \int_{0}^{\infty} \frac{ln(x)^2}{(1+x^2)(a^2+x^2)} \, \mathrm{d}x \] I= \[ \int_{0}^{\infty} \frac{ln(x)^2}{(1+x^2)} \, \mathrm{d}x \] a) exprimer J(a) en fonction de I, a et \[ \int_{0}^{\infty} \frac{ln(x)}{(1+x^2)}...

Bonjour à tous,

Comment montrer que l'image reciproque d'un segment par une fonction continue est une union de segments ?

Bonjour, Si le nombre de mains contenant un as au black-jack correspond au nombre de paquets de deux cartes contenant au moins un as alors tu t'es trompé je crois : quand tu tires la deuxieme carte y'a plus la première donc il reste 51 cartes : c'est pas exactement ce que t'as ecris Pour le nombre d...

Ah ouais merci ! J'ai pas vu la disjonction de cas ça permet d'enlever r+p/q je m'en rappelerai !

Ah ouais j'ai compris merci ! E c'est egal à p+sqrt(2) De là j'obtiens p-qsqrt(2) superieur ou egal à 1/(p+q*sqrt(2)) que je minore par 1/q en valeur absolu, et en divisant l'inegalite par q on obtient le resultat avec C=1 Edit: en fait je peux pas minorer par 1/q, mais ma minoration depend de p et ...

Merci beaucouo j'ai trouvé

p et q sont des entiers, donc p^2-2q^2 est un entier non nul, non nul de surcroît.

Alors p^2-2q^2 est superieur en valeur absolu à 1

Maitenant j'obtient preque l'inegalite avec cela mais j'ai le 2 au carré et pas de racine de 2, a partir de la on fait quoi svp ?

Merci pour la reponse j'ai montrer que racine de 2 est irrationnel en disant que s'il etait rationnel il existe des nombres premiers entre eux p et q tels que leur quotient fasse racine de 2, et en mettant au carre j'arrive au resultat Ainsi je peux ecrire que racine de 2 c'est un toujours un ration...