29 résultats trouvés
Revenir à la recherche avancée
Complexe barycentre
Bonjour Z_A=-1+i ; Z_B=1-i ; Z_C=1+3i G barycentre des point (A, 2)(B, 1)(C, 1) Calculer Z_G Déterminer et construire l'ensemble des points M du plan tel que -2MA^2+MB^2+MC^2=16 J'ai calculé Z_G =i Pour Déterminer l'ensemble des points M du plan tel que -2MA^2+MB^2+MC^2=16 -2(MG+GA)^2+(M...
- 01 Jan 2019, 12:31
- Forum: ✎✎ Lycée
- Sujet: Complexe barycentre
- Réponses: 2
- Vues: 186
Re: Intégrales suites
Pour la question 2.b
J'essaie de démontrer l'inégalité mais j'arrive pas
√2<= <=0
<=0
0<=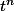 <=1
<=1
En faisant le produit je ne trouve pas les inégalités à démontré
J'essaie de démontrer l'inégalité mais j'arrive pas
√2<=
0<=
En faisant le produit je ne trouve pas les inégalités à démontré
- 30 Déc 2018, 19:58
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Re: Intégrales suites
Donc Pour démontré que la suite (In) est minoré je peux procédé de la même façon
J'ai sur [0; 1]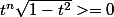 (1) et
(1) et 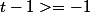 (2)
(2)
En faisant le produit (1)et(2) on à>=0)
Donc la suite In est minoré par 0
J'ai sur [0; 1]
En faisant le produit (1)et(2) on à
Donc la suite In est minoré par 0
- 30 Déc 2018, 19:06
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Re: Intégrales suites
J'ai pas mal de choses à votre absence 1a) Soit g [rouge]une[/rouge] primitive de \sqrt{1-x} f(x)=[g(x)]^{cosx}_0= g(cosx)-g(0) f'(x)=(g(cosx))'-(g(0))'= -sinx\sqrt{1-cos^2x} =-sinx|sinx| b) f(x)=\dfrac{1}{4}sin2x-\dfrac{x}{2}+c Or f(π/2)=0 => f(x)=\df...
- 30 Déc 2018, 18:19
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Limite
bonsoir s'il-vous-plaît pouvez-vous m'aider à calculer la limite de }{x}) en +oo
en +oo
Re: Intégrales suites
Soit g la primitive de 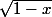
f(x)=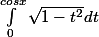 si g est la primitive de f
si g est la primitive de f
=[g(x)]^{cosx}_0= g(cosx)-g(0))
f'(x) =g'(cosx)-g'(0)=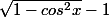
C'est correct la ?
f(x)=
f'(x) =g'(cosx)-g'(0)=
C'est correct la ?
- 28 Déc 2018, 17:28
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Re: Intégrales suites
Donc c'est vrai ce que j'avais fait f'(x) =g'(cosx) =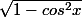
Ou bien j'ai oublié un truc ?
Ou bien j'ai oublié un truc ?
- 28 Déc 2018, 16:56
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Re: Intégrales suites
f(x)=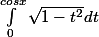 si g est la primitive de f
si g est la primitive de f
J'ai écris que=[g(x)]^{cosx}_0= g(0)-g(cosx))
Mais vous vous avez dit que f(x)=g(cosx)-g(cos0) vous avez fait comment
J'ai écris que
Mais vous vous avez dit que f(x)=g(cosx)-g(cos0) vous avez fait comment
- 28 Déc 2018, 15:29
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Fonctions
Soit la fonction f(x)=\dfrac{ln(x+1)}{x} 1.a) Démontré que l'équation f(x)=x admet une unique solution sur ]0; +\infty[ que l'on notera \alpha Montrer que \alpha\in]\frac{1}{2}; 1[ b) Montrer que si x\in]\frac{1}{2}; 1[ ; alors f(x)\in]\frac{1}{2}; 1[ 1) je voulais appliqué l...
Re: Intégrales suites
si g est la primitive de
Alors f(x)=g(cosx)-g(0)
f'(x) =g'(cosx)-g'(0)=}) -1
-1
Alors f(x)=g(cosx)-g(0)
f'(x) =g'(cosx)-g'(0)=
- 28 Déc 2018, 13:38
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Re: Intégrales suites
J'ai pas du tout compris
- 27 Déc 2018, 20:48
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Re: Intégrales suites
Bonjour On définit la suite (I[sub]n[/sub]) par I[sub]0[/sub] = \int_0^1\sqrt{1-t^2}dt et I[sub]n[/sub]= \int_0^1t^n\sqrt{1-t^2}dt pour tout n€IN 1)on pose f(x)= \int_0^{cosx }\sqrt{1-t^2}dt pour tout x€IR a)Montrer que f est derivable sur IR puis calculer f'(x) b) Déterminer f(x) pour x€[ 0; \frac{...
- 27 Déc 2018, 20:15
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Intégrales suites
Bonjour On définit la suite (I[sub]n[/sub]) par I[sub]0[/sub] =[tex]\int_0^1\sqrt{1-t^2}dt[/tex] et I[sub]n[/sub]=[tex]\int_0^1t^n\sqrt{1-t^2}dt[/tex] pour tout n€IN 1)on pose f(x)=[tex]\int_0^{cosx }\sqrt{1-t^2}dt[/tex] pour tout x€IR a)Montrer que f est derivable sur IR puis calculer f'(x) b) Déte...
- 27 Déc 2018, 20:14
- Forum: ✎✎ Lycée
- Sujet: Intégrales suites
- Réponses: 14
- Vues: 717
Re: Démonstration
[quote="Helenedupain"]Tout l'exercice c'était ça 1. Demontrer que : \forall x \in ]0 ; +\infty[, \frac{1}{x+1}<ln(\frac{x+1}{x})<\frac{1}{x}. En déduire que : \forall x \in ]0 ; +\infty[, (\frac{x+1}{x})^x<e<(\frac{x+1}{x})^{x+1}. 2. Démontrer que : \forall n \in $N...
- 20 Déc 2018, 15:33
- Forum: ✎✎ Lycée
- Sujet: Démonstration
- Réponses: 13
- Vues: 464
Re: Démonstration
Pour l'inégalité de gauche: poser la suite u_n=\ln{\frac{(n+1)^n}{n!}} et montrer par récurrence que u_n<n : \bullet \: u_1=\ln{2}<\ln{e}=1 \bullet montrer que pour n\geq1 on a (u_n<n \Rightarrow u_{n+1}<n+1) es que la ça suffirait pour conclure que c'est vrai au rang n+1? J'essaie d...
- 19 Déc 2018, 17:51
- Forum: ✎✎ Lycée
- Sujet: Démonstration
- Réponses: 13
- Vues: 464
Re: Étude de fonction
Ah merci
Comment je vais faire pour l'autre inégalités de dessous ?
Comment je vais faire pour l'autre inégalités de dessous ?
- 15 Déc 2018, 07:16
- Forum: ✎✎ Lycée
- Sujet: Étude de fonction
- Réponses: 6
- Vues: 297
Re: Étude de fonction
Demontrer que pour tout t de I on a:
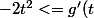 <=0) si t>=0
si t>=0
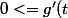 <=-2t^3 [) si -1/2<=t<=0
si -1/2<=t<=0
Comment pourrais-je démontré ça ?
Comment pourrais-je démontré ça ?
- 14 Déc 2018, 08:25
- Forum: ✎✎ Lycée
- Sujet: Étude de fonction
- Réponses: 6
- Vues: 297
Étude de fonction
Bonsoir tout le monde j'ai un exercice composé de 3 partie (A, B etC) Partie A On considère la fonction numérique g définie sur l'intervalle I= [-\dfrac{1}{2}; +\infty[ par g(x)=ln(1+x)-x+ \dfrac{x^2}{2}-\dfrac{x^3}{3} 1.Demontrer que pour tout t de I on a: -2t^2<=g'(t) <=0 si t>=0 0<=g&...
- 13 Déc 2018, 18:58
- Forum: ✎✎ Lycée
- Sujet: Étude de fonction
- Réponses: 6
- Vues: 297
Re: Démonstration
Merci beaucoup je comprends mieux la méthode de la récurrence
J'aimerais bien comprendre aussi la méthode avec les intégrales
J'aimerais bien comprendre aussi la méthode avec les intégrales
- 13 Déc 2018, 17:38
- Forum: ✎✎ Lycée
- Sujet: Démonstration
- Réponses: 13
- Vues: 464
Re: Démonstration
J'ai utilisé ce genre de méthode pour démontrer les inégalités de la question 1 f(x)=\dfrac{1}{x+1}-ln(\dfrac{x+1}{x}) f'(x)=-\dfrac{1}{(x+1)^2}+\dfrac{1}{x(x+1)} Or \dfrac{1}{x(x+1)}<\dfrac{1}{(x+1)} donc f'(x) <0 la fonction f est stricte...
- 13 Déc 2018, 15:17
- Forum: ✎✎ Lycée
- Sujet: Démonstration
- Réponses: 13
- Vues: 464
- 29 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
