Forum de Mathématiques: Maths-Forum

Si mon raisonnement a été compris, je suis d'autant plus satisfait. Merci.

Salut, J'ai un exercice qui me dérange car je n'arrive pas réellement a cerner ce qu'on me demande de faire. J'aimerais avoir quelques indications. Déterminer et représenter le plus grand domaine de définition possible des fonctions suivantes. a) f(x,y)=\ln (y-x^2) b) f(x,y)=...

Salut Celine62740, si on nomme Un la suite qui représente le salaire de cet employer. Ainsi en 2019, il recoit U_{0}=1500 , ensuite en 2020, il recoit U_{1}=1500+1500*(4/100) +20= 1500*1,04+20 qui représente en fait, U_{1}=U_{0}*1,04+20 , par suite U_{2}=U_{1}*1,04+20 . Si j'ai fait une bonn...

Salut, Je n'ai pas pu résoudre l'exercice suivant : L'écart type des poids d'une très grande population de personnes est 10 Kg. On extrait de cette population des échantillons de 200 personnes chacun. On calcule alors les écarts types pour chaque échantillon. (a) Trouver la moyenne et l'écart type d...

Salut, comment fait-on pour déterminer la partie symétrique et la partie antisymétrique d'une application bilinéaire dont sa matrice est diagonale?

Merci d'avance.

Ok, je vois!!

OK. mais si on prend P\cap Q, cela ne marche pas!??

Salut, J'ai commencé un exercice et j'ai eu certaines problèmes. L'exercice est le suivant : Prouver les propositions suivantes: \forall f, g \in \varepsilon_{[a,b]} : - fg \in \varepsilon_{[a,b]} ; - \sup (f,g) \in \varepsilon_{[a,b]} où \sup (f,g)(x) = \max {(f(x...

Salut, Je n'ai pas pu faire l'exercice suivant: Pour tout entier naturel n \le 2 , on note par S(n, 2) le nombre d'applications surjectives d'un ensemble E à n éléments vers un ensemble F à deux éléments. 1. Déterminer le nombre d'applications non surjectives de E vers F. 2. En déduire la va...

Salut, Je n'arrive pas a comprendre les propriétés suivantes et on me demande de les démontrer: Soit n et p deux entiers naturels. 1. Le nombre de n-uplets (x_{1}, ..., x_{n}) \in \mathbb{N}^{n} tels que x_{1}+ ... +x_{n}\le p est n+p\choose p . 2. Le nombre de n-uplets (x_{1}, ..., x_{n...

OK, merci beaucoup!!

La série de Fourier de f va s'écrire .

Salut, pour n pair, on a: et pour n impair, on a: 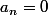. Pour pouvoir ecrire la serie de fourier, on va gérer le cas de 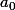comment?

Salut, je n'arrive pas a faire la question de 2 de l'exercice suivant: Soit f : \mathbb{R} \rightarrow \mathbb{R} la fonction 2 \pi - périodique définie par f(x)=|\cos(x)| . 1- Calculer les coefficients de Fourier trigonométriques de f. 2- En déduire la valeur de la somme \sum_{n=1}^...

Je ne comprends pas bien ton raisonnement.

Salut, en fait voici ce que dit le lemme dans notre cours. Soit f : \mathbb{R} \rightarrow \mathbb{R} la fonction 2 \pi - périodique et Riemann integrable sur [0, 2 \pi [. La suite des sommes partielles (S_{n})_{n} associé à la série de Fourier de f vérifie pour tous n\in \mathbb{N} et x \in...

Salut,
On me demande de montrer que en utilisant la formule de Dirichlet.

Merci d'avance.

Salut,
On me demande de montrer que en utilisant la formule de Dirichlet.

Merci d'avance.

Salut, On me demande dans un exercice: - Pour x\in]-1,1[ , calculer la somme de la serie \sum_{n\geq 1}{\frac{x^{n}}{n}} en utilisant le théorème sur l'intégrabilité terme a terme - Pour x\in]-1,1[ , calculer la somme de la serie \sum_{n\geq 1}{nx^{n-1}} en utilisant le théorème sur la dérivabilité ...

Salut LB2, tu calcules la largeur de comment?