Forum de Mathématiques: Maths-Forum

Bonjour, Je cherche à démontrer mathématiquement que exp(exp(n)) avec n entier, est supérieure (ou inférieure du coup) à n! (n factorielle). Dans ce genre de démonstration où les nombres sont astronomiquement énormes, quelles sont les astuces ? Car avec un logiciel comme géogébra, on ne peut pas tro...

Bonjour, Je dois résoudre cet exercice : Montrer que toute famille finie (Pi)1≤i≤m de polynômes non nuls, de degrés deux à deux distincts, est libre. Je sais personnellement que cela est vrai si la famille est échelonnée en degré. Mais là ce n'est pas le cas. L'affirmation semble logique, mais comme...

D'accord. Je viens de comprendre.
Merci beaucoup pour votre aide et votre patience, et surtout bonne année

x-y représente le Ker de f donc ?

Mais pourquoi cela prouve que f est injective ?

Donc ça donne : Supposons que ker(f) = { 0_{E} } Montrons que f est injective Soit x et y dans E f(x) = f(y) f(x) - f(y) = 0_{F} f(x-y) = 0_{F} par linéarité d'où 0_{E}=0_{F} Je ne comprends pas où est-ce que l'on utilise l'hypothèse que ker(f)...

Je ne comprends pas.
Pour montrer que f est injective, il faut que si f(x) = f(y) alors x=y non ?

Oki, merci aviateur pour tes réponses rapides et utiles

Bonjour tout le monde !
Pour finir 2018 en beauté ^^ on me demande de résoudre celà :

Soit E,F deux espaces vectoriels sur R et f : E -> F une application linéaire. Montrer que f est injective si et seulement si Ker(f) = {}.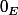

Je ne comprend pas comment faire.
Merci pour beaucoup votre aide

Okay, donc si j'ai bien compris aviateur, il n'existe que des petit rond de la forme o(x^n) ? Jamais on ne trouvera de chose plus complexe

Bien le bonjour mes chers, J'espère que tout va bien de votre côté et que le soleil perce tranquillement les nuages. De mon côté, que de brouillard ! Exemple : Le DL de arctan(x) en 0 à l'ordre 3 est tout simplement : arctan(x) = x - \frac{1}{3}x^{3}+o(x^3) Tout va bien. Mais mainten...

Oyez tout le monde, J'espère que tout va bien de votre côté. Du miens, je ne comprend pas comment trouver la réponse à cette question : C'est un problème de physique mais comme on ne peut pas utiliser les énergies cinétiques ou potentielles, je pense qu'il y a une subtilité cachée. On s'intéresse à ...

Excusez-moi ...
Soit une fonction continue

Bonjour la compagnie,
J'espère que chez vous tout rayonne !
De mon côté, il pleut :

Démontrer que pour tout , il existe tel que

Je ne comprend pas quels outils utilisés...

Merci pour votre aide précieuse

ô grand merci, sincèrement.

Bonsoir et catastrophe !



Je suis dépité ... Je ne vois pas quoi faire ... Pas de factorisation, pas de taux d'accroissement, pas d'encadrement, pas de changement de variable ...

Apporter moi le savoir que la vie ne m'a pas donné.

Merci

Whouaa
Merci beaucoup mathelot pour ta réponse complète et rapide

Oyez braves gens. Par ce beau dimanche, me voilà tombé sur un os. Soit P une fonction polynomiale. Démontrer que \lim_{x\rightarrow +\propto } P(X) e^{-x} = 0 En soit, ça parait évident. La fonction exponentielle est la "plus forte". Mais comment le démontrer ? Merci pour vos répon...

Ah oui !
Merci beaucoup mathelot

Merci pour ta réponse rapide ;-) Voici mon développement : (cosx+isinx)^3 = cos^3x+3cos^2x * i sinx + 3cosx * (isinx)^2+(isinx)^3 = cos^3x - 3cosx*sin^2x + i (3cos^2x * sinx - sin^3x) J'ai donc ma partie imaginaire, mais elle n'est pas sous la forme que tu m'as donnée...

Bien le bonjour les matheux ! "On a sin(3x) = Im[(cos(x) + i sin(x))^3] (pourquoi ?). En déduire que l’on a sin(3x) = P(sin(x)) , où P est un polynôme que l’on déterminera." En voilà une bonne question ^^ Donc pour le "pourquoi&q...