oui merci pour la remarque
donc pour éviter de tomber dans ce cas que vous avez mentionner on ajoute la condition de continuité et ca sera suffisant n'est ce pas ????
23 résultats trouvés
Revenir à la recherche avancée
- 23 Juin 2020, 19:44
- Forum: ✎✎ Lycée
- Sujet: fonction décroissante et sa limite en + infini est positive
- Réponses: 6
- Vues: 1025
fonction décroissante et sa limite en + infini est positive
Salut
j'ai une petite question : si on a une fonction g décroissante et sa limite en + infini est un réel positif . est ce que ceci est suffisant pour dire que la fonction g est positive sinon c'est quoi le contre exemple dans ce cas
merci d'avance pour vos réponses
j'ai une petite question : si on a une fonction g décroissante et sa limite en + infini est un réel positif . est ce que ceci est suffisant pour dire que la fonction g est positive sinon c'est quoi le contre exemple dans ce cas
merci d'avance pour vos réponses
- 23 Juin 2020, 18:21
- Forum: ✎✎ Lycée
- Sujet: fonction décroissante et sa limite en + infini est positive
- Réponses: 6
- Vues: 1025
Re: mesure de l'angle dont on connait son sin et cos
Bonjour, Salut J'ai une question : Si la valeur de cos a = -3/5 et sin a = -4/5 alors que vaut la mesure de l'angle en radian ? ; j'utilise la calculatrice ( cos ^-1 et sin^-1) j'obtient deux valeurs différentes . Avec ces deux valeurs on a bien cos^2 a + sin^2 a = 1 donc ces deux valeurs sont cohé...
- 09 Fév 2020, 13:43
- Forum: ✎ Collège et Primaire
- Sujet: mesure de l'angle dont on connait son sin et cos
- Réponses: 6
- Vues: 584
Re: mesure de l'angle dont on connait son sin et cos
Dans ce cas j'obtient a= 0.92 mais a appartient à [-pi ; -pi /2 ] alors a = pi -0.92 ; C'est ça ou pas ?
Merci pour la réponse
Merci pour la réponse
- 09 Fév 2020, 13:37
- Forum: ✎ Collège et Primaire
- Sujet: mesure de l'angle dont on connait son sin et cos
- Réponses: 6
- Vues: 584
mesure de l'angle dont on connait son sin et cos
Salut
J'ai une question : Si la valeur de cos a = -3/5 et sin a = -4/5 alors que vaut la mesure de l'angle en radian ? ; j'utilise la calculatrice ( cos ^-1 et sin^-1) j'obtient deux valeurs différentes .
J'ai une question : Si la valeur de cos a = -3/5 et sin a = -4/5 alors que vaut la mesure de l'angle en radian ? ; j'utilise la calculatrice ( cos ^-1 et sin^-1) j'obtient deux valeurs différentes .
- 09 Fév 2020, 12:47
- Forum: ✎ Collège et Primaire
- Sujet: mesure de l'angle dont on connait son sin et cos
- Réponses: 6
- Vues: 584
dérivabilité
Bonjour ,
En lisant la définition de dérivabilité d'une fonction je trouve qu' on se situe toujours dans un intervalle ouvert . Pourquoi exactement on pose cette condition ?
Merci d'avance pour tout éclaircissement,
En lisant la définition de dérivabilité d'une fonction je trouve qu' on se situe toujours dans un intervalle ouvert . Pourquoi exactement on pose cette condition ?
Merci d'avance pour tout éclaircissement,
- 24 Oct 2019, 12:41
- Forum: ✯✎ Supérieur
- Sujet: dérivabilité
- Réponses: 4
- Vues: 214
Re: preuve à une implication
Salut, Déjà, vu que |a|<1 et |b|<1 on a |ab|<1x1=1 c'est à dire -1<ab<1 et ça prouve en particulier que 1+ab>0 et donc que |1+ab|=1+ab. Ensuite, montrer que |a+b| < 1+ab, ça revient très précisément à montrer que -(1+ab) < a+b < 1+ab, c'est à dire que 1+ab+a+b > 0 et que 1+ab-a-b >0 [du fait de la ...
- 31 Aoû 2019, 21:11
- Forum: ✎✎ Lycée
- Sujet: preuve à une implication
- Réponses: 4
- Vues: 861
Re: preuve à une implication
Merci infiniment votre réponse était bien claire , j'ai pu démontrer le reste . Merci encore une fois
- 31 Aoû 2019, 21:10
- Forum: ✎✎ Lycée
- Sujet: preuve à une implication
- Réponses: 4
- Vues: 861
preuve à une implication
Bonsoir tout le monde
je cherche à prouver que quelque soit deux réel a et b dans R
si |a| <1 et |b| <1 alors |a+b| <|1+ab|
je sais pas d'ou commencer , j'aimerais avoir vos idée
Merci d'avance
je cherche à prouver que quelque soit deux réel a et b dans R
si |a| <1 et |b| <1 alors |a+b| <|1+ab|
je sais pas d'ou commencer , j'aimerais avoir vos idée
Merci d'avance
- 31 Aoû 2019, 20:38
- Forum: ✎✎ Lycée
- Sujet: preuve à une implication
- Réponses: 4
- Vues: 861
Re: Encadrement
si (4/3) est une valeur approchée à (5/6) de x, on a : -(5/6) <x - (4/3) <(5/6) c'est aussi (4/3)-(5/6) <x < (4/3)+(5/6) on en déduit un premier intervalle pour la valeur approchée supposée il faut vérifier que ]1/2; 2/3[ soit bien inclus entièrement dans l'intervalle au-dessus Ton écriture est jus...
- 25 Déc 2018, 19:35
- Forum: ✎✎ Lycée
- Sujet: Encadrement
- Réponses: 2
- Vues: 272
Encadrement
Bsr ! J'ai une petite question si vous pouvez me répondre On cherche à prouver que \frac{4}{3} est une valeur approché de x à précision \frac{5}{6} Sachant que x appartient à l'intervalle ] \frac{1}{2} ; \frac{3}{2} [ Quand je fais l'encadrement j'arrive à : \frac{-5}{6} <x- \frac{4}{3} < \frac{1}{6...
- 24 Déc 2018, 20:27
- Forum: ✎✎ Lycée
- Sujet: Encadrement
- Réponses: 2
- Vues: 272
Re: Barycentre 1 er S
beka a écrit:Oui j 'ai pensé de faire ca et j'ai obtenumais puis pour qu'elle soit colinéaire avec
il faut
et je bloque . ca sera quoi le système des points dans ce cas
- 04 Déc 2018, 18:49
- Forum: ✎✎ Lycée
- Sujet: Barycentre 1 er S
- Réponses: 4
- Vues: 308
Re: Barycentre 1 er S
Oui j 'ai pensé de faire ca et j'ai obtenu  mais puis pour qu'elle soit colinéaire avec
mais puis pour qu'elle soit colinéaire avec 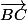 il faut
il faut 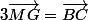 et je bloque . ca sera quoi le système des points dans ce cas
et je bloque . ca sera quoi le système des points dans ce cas
- 04 Déc 2018, 18:48
- Forum: ✎✎ Lycée
- Sujet: Barycentre 1 er S
- Réponses: 4
- Vues: 308
Barycentre 1 er S
bsr a tous j'ai besoin de l'aide s'il vous plait dans cette question ,
Déterminer l'ensemble E des points M du plan (P) tels que :
 est colinéaire avec
est colinéaire avec 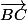
je sais d'ou commencer quelqu'un à m'aider
Déterminer l'ensemble E des points M du plan (P) tels que :
je sais d'ou commencer quelqu'un à m'aider
- 04 Déc 2018, 17:56
- Forum: ✎✎ Lycée
- Sujet: Barycentre 1 er S
- Réponses: 4
- Vues: 308
Ordre dans R
salut a tous ; je me trouve bloqué devant cette démonstration ; on a x> 1 et y>1
Prouver que x+y < 2xy
J'ai essayé de jouer avec les identités remarquable mais je trouve : x+y > 2
j'aimerais bien recevoir de l'aide . Merci d'avance
Prouver que x+y < 2xy
J'ai essayé de jouer avec les identités remarquable mais je trouve : x+y > 2
j'aimerais bien recevoir de l'aide . Merci d'avance
- 02 Déc 2018, 12:05
- Forum: ✎✎ Lycée
- Sujet: Ordre dans R
- Réponses: 4
- Vues: 276
Preuve d'une egalité
Salut voici une question qui me casse la tete pas mal de temps a,b,c dans R montrer que (a-b)^3+ (b-c)^3+(c-a)^3=3(a-b)(b-c)(c-a) J'ai fait des calculs ,j'arrive a montrer que (a-b)^3+ (b-c)^3+(c-a)^3=3[a^2(c-b)+b^2(...
- 18 Nov 2018, 19:19
- Forum: ✎✎ Lycée
- Sujet: Preuve d'une egalité
- Réponses: 1
- Vues: 204
Egalité de deux fonction
Bsr a tous ! j'ai un petit soucis concernant l'écriture f(x)=\sqrt \frac {x-1}{x+1}=\frac {\sqrt {x-1}} {\sqrt {x+1}} Est ce que l'égalité précédente est juste sachant que la fonction f(x)= \sqrt \frac {x-1}{x+1} est différente de g(x)= \frac {\sqrt {x-1}} {\sqrt {x+1}} car ils ont pas le mê...
- 09 Nov 2018, 20:20
- Forum: ✎✎ Lycée
- Sujet: Egalité de deux fonction
- Réponses: 1
- Vues: 521
Re: Arithmetique - difference de deux carre parfait
Salut, tu as pourtant donné toute la démarche. n^2+n+7=2\frac{n^2+n+6}{2}+1 ( \frac{n^2+n+6}{2} est bien un entier) Et maintenant tu as ton fameux "2k+1", et comme tu l'as dit toi même que 2k+1=(k+1)^2-k^2 , bha tu as finis. merci bcp tu m'a aidée Tellement j'ai compliqué les chos...
- 31 Oct 2018, 14:34
- Forum: ✎✎ Lycée
- Sujet: Arithmetique - difference de deux carre parfait
- Réponses: 2
- Vues: 557
Arithmetique - difference de deux carre parfait
Salut les matheux Voila un petit problème que j'ai rencontré et je suis bloquée je cherche d'écrire n^2 + n+7 sous forme de différence de deux carrées consécutifs Sachant que n^2 + n+7 est un nombre impairs et tout nombre impairs est différence de deux carrées parfaits consécutifs : (x^2+1)-x^2 = 2x...
- 31 Oct 2018, 14:17
- Forum: ✎✎ Lycée
- Sujet: Arithmetique - difference de deux carre parfait
- Réponses: 2
- Vues: 557
Re: Inequation
Oui, c'est ça et le h=b-a, c'est uniquement pour économiser un peu d'encre et pour mieux visualiser l'hypothèse b>a : si on pose h=b-a, cette hypothèse s'écrit h>0 ce qui est "plus visuel". Et vu que cette preuve est totalement "bétassou" et tient une ligne, j'aurais tendance à ...
- 18 Oct 2018, 19:20
- Forum: ✯✎ Supérieur
- Sujet: Inequation
- Réponses: 6
- Vues: 425
- 23 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
