Forum de Mathématiques: Maths-Forum

Lol ! Je me suis emballé ? C'est si compliqué ? Si c'est difficile, ou puis-je trouver une solution ?

Salut,
J'aimerais calculer la fonction gamma, à partir de sa définition en intégrale. J'ai pensé à une intégration par parties, mais j'ai l'impression que cela me mène à rien. Y a-t-il une astuce ?
Merci d'avance de prendre le temps de me répondre.
++

Salut,
J'aimerais savoir si pour une fonction génératrice G, d'une variable aléatoire X, telle que G(t)=E( ), il est possible, pour un réel r et une variable W,tels que X=r+W, d'écrire G(t)=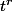E( )= E( ).
Et si oui, pourquoi ?
Merci d'avance.

Salut,
je cherche à calculer l'intégrale suivante :
. En faisant une intégration par parties, j'obtiens 0 :hum:
Je pense pas que ce soit ça, pourriez-vous m'aider.
Merci d'avance.

Salut
J'ai un petit problème de récurrence:
Soit ma proposition : rec(0,n+1)>=rec(0,n)+rec(0,n-1)
J'aimerais la montrer au rang n+1 mais je bloque stupidement.
Pourriez-vous m'aider.
++

Salut, je me pose des questions sur la différentiabilité parce que là je m'embrouille. Pour montrer qu'une fonction est différentiable en un point b, je peux montrer que ses dérivées partielles sont continues en ce même point, mais avant cela, dois-je montrer que ces dérivées partielles existent ? C...

Salut, Je recherche des livres traitant de l'histoire des mathématiques.C'est à dire leur apparition, leur emploi au cours de l'histoire (ce que j'aime beaucoup ce sont les croquis,dessins de figures mathématiques, donc si en plus y'en a )... S'il y en a parmi vous qui en avez des biens à me conseil...

Mais là je suis perdu, je m'appretais a faire a/(x+1) + b/(x+1) , je ne comprends plus , pourquoi met on le premier dénominateur à la puissance de 2, et pas le deuxieme ?Je regardé sur wikipédia,et la méthode de fahr451 mais je comprends pas vraiment, dans mon cours j'ai du alpha, du beta,du a ... j...

Ouh la, pas mal de calcul ,je trouve sa bizarre, peut etre je me suis trompé quelque part ? Pourriez pour m'aider, me montrer comment calculer l'intégrale de 0 à 1 de la fonction (2x-1)/(x+1)^2, car je trouve que (2x-1)/(x+1)^2=a/(x+1)+b/(x+1) mais alors après pour trouver le a et b :doh: pourtant j...

J'ai une ultime question !!! comment je peux factoriser 2u^2+u+2 ? car pour l'intégrale ou je pose i=tan(x/2) j'obtiens 2du/(2u^2+u+2) ,donc je remarque que c'est une fonction rationnelle, mais j'arrive pas a factoriser.
merci encore de tout mon coeur :we:

ok ok, j'ai un dernier problème :cry: pour la première intégrale de fraction rationnelle, j'obtiens que x^3/(x^2+x-2)=a/(x-1)+b/(x+2) mais comment je résoud ? le x^3 me pose problème après.
merci beaucoup de prendre le temps de me répondre.
++

Merci pour vos réponses. J'ai une derniere question, dans mon premier post, pour la deuxième intégrale, je pose donc u=tan(x/2), jarrive à écrire l'intégrale sous la forme (2du/(1+u^2))*(1/(2+sinx)). Comment je peux faire pour transformer mon sinx en quelquechose de u ?

Et pour calculer les intégrales suivantes je fais comment ? \int_(-1)^{0} x^3/(x^2+x-2) dx \int_0^{1} (2x-1)/(x+1)^2 dx Je vois que ce sont des fonctions rationnelles mais je n'ai pas compris comment on faisait pour l'exprimer en fonction de a, b et c.Pouvez-vous m'ai...

Salut, je bloque pour calculer des intégrales, car je ne trouve pas le changement de variable; auriez-vous une astuce pour que je trouve facilement le changement à faire parce que pour moi, j'ai l'impression qu'il faut beaucoup d'intuition pour le trouver. Voici mes intégrales : int_pi/3^{pi/2} dx/&...

Ok, mais pour la question 3) je rebloque; comment faire svp ?

Mais je fais comment pour la première question ? je crois qu'il faut utiliser une matrice de passage mais de quelle base à quelle base puisque l'on a que la base canonique ?

Voilà, j'ai un petit problème avec un exercice, je suis pas sur des mes réponses, et je bloque pour certaines questions.Je vous remercie d'avance de prendre le temps de m'aider. Soit g: \mathbb{R} [X]-> \mathbb{R} [X] P(X)-> g(P)(X)=P(X+1) g une application linéaire, on note g _n sa restriction à \m...

Ok, je vois un peu mieux, mais comment je pourrais en conclure que f' vérifie la propriété des valeurs intermédiaires ?

Salut, j'ai un petit problème pour une question d'un exo,voici l'énoncé : Soit I un intervalle de R et f une fonction de I dans R dérivable sur I. Soient a et b appartiennent à un I de R et a<b. On suppose que f'(a)f'(b)<0 On définit les fonctions p et q telles que p(x)= (f(x)-f(a))/(x-a) si x diffé...