Forum de Mathématiques: Maths-Forum

Ok je tente en plus simplifier On suppose N' continue Pour tout x pour tout \epsilon > 0 il existe \delta > 0 telle que pour tout y N(x-y) < \delta ==> | N'(x) - N'(y)| < \epsilon Je pose x = 0 et \epsilon = 1, on a alors que N(y) < \delta ==> N'(y) < 1 Pour u différent de v Je pose y = ( \delta *(u...

Bonjour, Oui je vois que tu veux dire je me rappelle m'être fais la réflexion mais que par fainéantise ne pas avoir changer le x après avoir commencer avec et t'avoir écris vite ce que j'avais fais sans réfléchir. Je refait tout ça. N' (l'appiation de (b) ) continue Pour tout x pour tout \epsilon > ...

Pour (b) implique (c): J'ai pour tout \epsilon > 0 il existe \delta > 0 telle que N(x-y) < \delta implique |N'(x) - N(y)| < \epsilon Je prend alors \epsilon = 1 et je regarde N(( \delta *(x-y))/(2*N(x-y))) c'est égale à \delta /2 qui est bien inférieur à \delta J'ai alors que |N'(( \delta *x)/(2*N(x...

Je viens de penser à quelque chose, si je prend y = 0, j'ai alors
|N'(x) - N'(0)| K * N(x-0)
comme N' est une norme alors N'(0) = 0
qui donne N'(x) K* N(x) pour tout x appartenant à V
cela est-il correct pour prouver mon implication?

Pour (c) N' application de (V,N) dans R lipschitzienne cela donne: Pour tout x,y appartenant à V il existe K une constante strictement positive telle que | N'(x) - N'(y) | \leq K * N(x-y) et pour (d) N domine N' Pour tout v appartenant à V il existe une constante C strictement positive telle que N'(...

Bonjour, Je suis entrain de faire un exercice où le but et de montrer l'équivalence de proposition. J'ai presque fini mais il me manque une implication pour conclure. Voici l'exercice: Soit N et N' deux normes de l'espace vectoriel V, montrer l'équivalence des propriétés suivantes. (a) l'identité de...

Merci

Bonjour, Je n'arrive pas à faire un exercice, un peu d'aide ne serai pas de refus: On considère un espace vectoriel normé V et un ouvert O de V distinct de V. (a) Montrer que pour tout point a de O, l'ensemble des \varepsilon > 0 tels que la boule ouverte centrée en a et de rayon \varepsilon inclus ...

Bonjour, Je suis bloqué sur une question, la voici : On suppose W un sous-espace vectoriel de dimension finie dans V, on fixe x \in V\W et on appelle m l'infinimum de \parallel v - w \parallel pour w \in W. La question est : Montrer qu'il existe au moins un w1 \in W tel que \parallel v -w1 \parallel...

Merci c'était bien ça ma question, pour mon contre exemple j'avais pris la tribu engendré par B mais en effet en prenant la tribu trivial avec B = Omega c'est beaucoup plus simple

Merci pour la deuxième question je comprends mieux.

Pour la première question les hypothèses sont que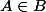 et que B appartient à F une tribu sur un espace omega.
Et à partir de ces deux hypothèses on doit dire si c'est vrai ou faux que A appartient à F.

Bonjour, Mon contre exemple fonctionne-t-il? Soit A \subset B deux ensembles et F une tribu telle que B \in F alors A \in F. Le contre exemple : En prenant F la tribu engendrée par B, par les unions et les complémentaires possibles avec les éléments de F on ne peut pas obtenir A alors on prouve que ...

Merci je comprends beaucoup mieux maintenant

Perso j'utilise A^{T} je viens de calculer la dériver, j'obtiens : E'(\alpha + t*h) = (Ah)^{T} * ( A * \alpha + A*t*h - b) + (A * \alpha +A*t*h - b)^{T} * (Ah) et donc en posant t = 0 E'(\alpha) = (A*h)^{T}*(A *\alpha - b) + ...

Bonjour, Je bloque complément sur un exercice, j'aurais besoin d'aide, tout est à valeurs dans R. Soit une matrice A à m lignes et n colonnes et un vecteur b à m coefficients. Pour tout x à m coefficients, on pose : E(x) = N(Ax-b)_{2}^{2} (la norme 2 au carré de Ax-b) Alors il faut montrer que pour ...

Merci !

Bonjour, J'ai vu que tout sous ensembles infini d'ensemble dénombrable est dénombrable. La définition de dénombrable étant que si E est en bijection avec N (entier naturels) alors E est dénombrable or dans la démonstration donnée dans mon cours et certaines que j'ai vu sur internet, ils montrent que...

Merci !

J ai du mal exprimer ma question. Je demandais si on a (A * A^T)_ij = (Somme pour k de 1 à n ) a_ik * a_jk Ou bien (A * A^T)_ij = (Somme pour k de 1 à n ) a_ik * a_kj Car pour un ami c est la deuxième qui est bonne alors que pour moi c est la première qui est exacte car pour moi la deuxième représen...

Bonjour, J'ai un petite question. Je prend un matrice carré A de rang n avec comme coefficients de A : a_ij. Si j'applique le produit matricielle à A avec sa transposée, noté A^T, alors les coefficients de cette matrice obtenue, que je note ici (A * A^T)_ij, valent-ils? (A * A^T)_ij = ( Somme pour k...