Forum de Mathématiques: Maths-Forum

super merci à vous tous,
discussion résolue
Je crois que ces résultats sont aussi valables pour r, le reste de

Merci pour la réponse,

pourquoi ?

justement, ma question était : comment prouver que 1 <= N2/N3<10 ?

catamat a écrit:par ex : et
1

car

ce n'est pas ça ?

Je vais essayer de remettre tout ça en ordre :
le diviseur N3 a n chiffres.
N2, le nombre des n premiers chiffres du dividende tel que . Avons-nous
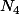
si alors on prend qui a n+1 chiffres. Avons-nous

Excuse-moi Ben314, mais je me suis gouré dans les hypothèses :
on a le dividende
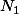
on a
on a le diviseur

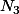
et on cherche à savoir si
quelqu'un a une idée?

Si on veut diviser N_1 par N_3 et que la différence du nombre de chiffres de N_1 et de N_3 est supérieur à 1, on prend le nombre N_2 au minimum des premiers chiffres de N_1 tel que N_{2} > N_3 et on ne considère pas les autres chiffres de N_1 . Puis on concatène les autres chiffres de N_1 au reste e...

Je me suis gouré, il faut remplacer x_{1} par x_{0} Soit N_{1} un nobre entier de n chiffres N_{1}=x_{0}+x_{1}*10+x_{2}*10^{2} +...+x_{n-1}*10^{n-1} Soit N_{2} le nombre constitué des n-1 premiers chiffres de N_{1} N_{2}=x_{1}+x_{2}*10+x_{3}*10^{2}+x_{4}*10^{3} +...+x_{n-1}*10^{n-2} N_{3} , le divis...

je voulais dire

Soit N_{1} un dividende de n chiffres : N_{1}=x_{0}+x_{1}*10+x_{2}*10^{2} +...+x_{n}*10^{n} Soit N_{2] un nombre constitué des n-1 premiers chiffres de N_{1} N_{2}=x_{1}+x_{2}*10+x_{3}*10^{2}+x_{4}*10^{3} +...+x_{n}*10^{n-1} N_{3} , le diviseur, est un entier tel que N_{2} < N_{3} on constate que N_...

car et sont des entiers?
l'exemple est général ?

Merci beaucoup, ça marche.

Peut-on généraliser ce cas (n'importe quel nombre de chiffres pour le dividende et le diviseur) ?

je comprends bien , mais pourquoi ?

Et si les trois premiers chiffres du dividende forment un nombre plus grand que le diviseur, comment démontrer que le rapport est inférieur à 10 ?

Merci pour la réponse a,b,c,d sont les chiffres d'un dividende et ABC les chiffres d'un diviseur si le diviseur a trois chiffres et que les 3 premiers chiffres du dividende forment un nombre inférieur au diviseur, alors on prend les quatre chiffres du dividende. Un nombre de quatre chiffres est forc...

on a N1=a*1000 + b*100 + c*10 +d
N2=a*100+b*10+C
N3=A*100 + B*10 +C
N2<N3
N1>N3
je pense que N1/N3 <10
comment le démontrer ? (démontrer que c'est vrai ou démontrer que c'est faux)
une idée ?

Si on continue, ça donne pour l'espace à 3 dimensions: x=x_A(1-k_1-k_2-k_3)+k_1 x_B + k_2 x_c + k_3 x_D y=y_A(1-k_1-k_2-k_3)+k_1 y_B + k_2y_c + k_3 y_D x=z_A(1-k_1-k_2-k_3)+k_1 z_B + k_2 z_c + k_3 z_D t=t_A(1-k_1-k_2-k_3)+k_1 t_B + k_2 t_c + k_3 t_D avec \vec{AB} et \...

je pensait que l'équation paramétrée d'une droite dans un espace à 4 dimensions serait: x=x_A (1-k)+ k x_B y=y_A (1-k)+ k y_B z=z_A (1-k)+ k z_B t=t_A (1-k)+ k t_B car \vec{AB}=k \vec{AM} pour un plan ça donnerai: x=x_A ( 1-k_1-k_2)+k_1 x_B+k_2 x_C y=y_A (...

Bonjour, j'aurai besoin de savoir comment passer de cette équation: x=\frac{1}{2}(x_{A}(1-k_1-k_2)+k_1 x_B+k_2 x_C+ x_D (1-k_3-k_4)+k_3 x_E+k_4 x_F) à celle-ci: x=X_1 ( 1-K) + K X_2 c'est pour démontrer que deux plans se croisent en une droite dans un espace à 3 dimen...

je rappelle le jugement majoritaire: https://fr.wikipedia.org/wiki/Jugement_majoritaire on a le map score qui indique le nombre d'électeurs qui ont donné un jugement à chaque candidat. std::map<std::string,int[6]>scores; par exemple, si on a les bulletins: candidats Toto,Titi,Tata bulletins tresbien...