29 résultats trouvés
Revenir à la recherche avancée
Re: DM math
Bonjour pour la question1) Montrer que les fonctions polynômes f_1 et f_2 définies pour tout x \in \mathbb_{R} f(x) = 2x^2 - 3x + 1 et par f_2(x) = x^2 - \frac{3}{2} x + \frac{1}{2} ont les mêmes racines. j'ai mis f_{1}(x) = 2x^2 - 3x + 1 =2 \left[x^2 - \frac{3}{2}x + \frac{1...
Re: DM math
Bonjour oui, c'est vrai \frac{b^2}{4a^2} - \frac{b^2 - 4ac}{4a^2} ce qui signifie ( avec la parenthèse ) \frac{b^2}{4a^2} - \frac{\left(b^2 - 4ac\right)}{4a^2} = \frac{b^2}{4a^2} +\frac{-b^2 + 4ac}{4a^2} \frac{b^2}{4a^2} + \frac{-b^2 + 4ac}{4a^2} = \frac{b^2 - b^2 + 4ac}{4a^2} b au carré moi...
Re: DM math
Bonjour pour la question1) Montrer que les fonctions polynômes f_1 et f_2 définies pour tout x \in \mathbb_{R} f(x) = 2x^2 - 3x + 1 et par f_2(x) = x^2 - \frac{3}{2} x + \frac{1}{2} ont les mêmes racines. j'ai mis f_{1}(x) = 2x^2 - 3x + 1 =2 \left[x^2 - \frac{3}{2}x + \frac{1...
Re: DM math
Bonsoir
moins devant une parenthèse donc ......
}{2a} =)
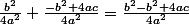
-
moins devant une parenthèse donc ......
-
Re: DM math
je dois avoir 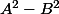 donc ....
donc ....
c'est pas si simple que ça
c'est pas si simple que ça
Re: DM math
Bonjour u \times v = \left(\frac{- b - \sqrt{b^2 - 4ac}}{2a}\right) \times \left(\frac{-b + \sqrt{b^2 - 4ac}}{2a}\right) pour trouver (A - B ) \times (A + B) = A^2 - B^2 je pose : A = -\frac{b}{2a} et B = \left(\frac{ \sqrt{b^2 - 4ac}}{2a}\right) -
Re: DM math
Bonjour u + \frac{b}{2a} + \frac{\sqrt{b^2 - 4ac}}{2a} = 0 \iff u = -\frac{b}{2a} -\frac{\sqrt{b^2 - 4ac}}{2a} = 0 \iff u = \frac{-b - \sqrt{b^2 - 4ac}}{2a} v + \frac{b}{2a} -\frac{\sqrt{b^2 - 4ac}}{2a} = 0 \iff u = -\frac{b}{2a} + \frac{\sqrt{b^2 - 4ac}}{2a} = 0 \iff u = -\frac{b +\sqrt{b^2 - 4ac}}...
Re: DM math
donc j'ai une multiplication de deux fractions par conséquent je multiplie les dénominateurs et les numérateurs u \times v = \frac{- b - \sqrt{\Delta}}{2a} \times \frac{- b + \sqrt{\Delta}}{2a} \frac{\left(- b - b^2 - 4ac\right) \times \left(- b + b^2 - 4ac\right)}{2a \times 2a} doub...
Re: DM math
multiplication de deux fractions
donc je multiplie les numérateurs et les dénominateurs
mon u c'est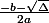
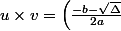 \times \left(\frac{- b +\sqrt{\Delta}}{2a}\right))
-
donc je multiplie les numérateurs et les dénominateurs
mon u c'est
-
Re: DM math
je dois obtenir c/a
il y a la lettre 'c' dans l'expression de
-
Re: DM math
u + v \frac{-b - \sqrt{\Delta}}{2a} + \frac{-b + \sqrt{\Delta}}{2a} les fractions ont le même dénominateur, j'additionne les numérateurs \frac{-b - \sqrt{\Delta} + - b + \sqrt{\Delta}}{2a} je peux simplifier les racines de delta soit : \frac{-b - b }{2a} me donne \frac{-2b}{2a} que je peux simplifie...
Re: DM math
Bonsoir et merci
Oui, j'ai re-démontré les formules du cours et je l'ai fait sans regarder le cours
Etes-vous sur qu'il n'y a pas d'erreurs dans les équivalents que j'ai écrites ?
Oui, j'ai re-démontré les formules du cours et je l'ai fait sans regarder le cours
Etes-vous sur qu'il n'y a pas d'erreurs dans les équivalents que j'ai écrites ?
Re: DM math
je pars de : ax^2 + bx + c = 0 mise en facteur de a et j'arrive à : ax^2 + bx + c = 0 <=> a \left[x^2 +\frac{b}{a}x + \frac{c}{a} \right] = 0 Je factorise : a \left[x^2 +\frac{b}{a}x + \frac{c}{a} \right] = a \left[\left(x^2 + \frac{b}{2a}x\right)^2 - \left(\frac{b}{2a}\right)^2 + \f...
Re: DM math
alors :
soit :
et j'ai une fonction affine, c'est à dire une droite donc pas de racines
-
Re: DM math
et bien 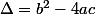
Re: DM math
Bonjour et merci pour l'aide Désolé, mais je ne comprends pas : une condition nécessaire et suffisante sur les coefficients d'une équation de second degré pour qu'elle admette des racines réelles. d'après mon cours tout ce que je comprends , c'est ça : si \Delta > 0 alors il y a deux racines si \Del...
Re: DM math
Bonjour J'ai besoin de conseil pour démontrer que f_1(x) = 2x^2 - 3x + 1 et f_2(x) = x^2 - \frac{3}{2}x + \frac{1}{2} ont les memes racines j'ai pensé suivre ce plan : - je démontre la raison qui fait que f_1(x) = 0 - je prouve qu'il y a proportionnalité entre les deux foncti...
Re: DM math
Bonjour,
je galère total sur ce DM et j'aimerais pouvoir progresser en mathématique.
Pouvez-vous m'aider ? s'il vous plait
je galère total sur ce DM et j'aimerais pouvoir progresser en mathématique.
Pouvez-vous m'aider ? s'il vous plait
Re: DM math
pour la question 1) j'ai fait ces calculs : f_1(x) = 2x^2 - 3x + 1 = 0 \Delta = b^2- 4 ac = (-3)² - 4 \times 2 \times 1 = 9 - 8 = (1)^2 x_1 =\frac{3 + 1}{4} = 1 x_2 =\frac{3 - 1}{4} = \frac{2}{4} = \frac{1}{2} f_2(x) = x^2 - \frac{3}{2}x + \frac{1}{2} = 0 a = 1 , b = ...
- 29 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
