Forum de Mathématiques: Maths-Forum

guillaume100 a écrit:Bonsoir,

Soit f la fonction qui à x associe x*(1+x) sur R+
Tu la dérives et tu trouves qu’elle est strictement croissante, donc f(a)=f(b) implique que a=b car elle est strictement croissante. Or de f(a)=f(b) équivaut à ton équation sur R+ en divisant voila

merci infiniment.

En utilisant les définitions, montrer :
A different de B si et seulement s’il existe a dans A\ B ou b dans B\ A.

guillaume100 a écrit:Ouais bien vu,
Sinon tu dis que la fonction qui à x associé x*(1+x) est strictement croissante

bonsoir
tu peux expliquez plus stp.

A\bigcap{} (B\bigcup{}C) = (A\bigcap{B}) \bigcup{} (A\bigcap{C}) pour montrer ceci on doit montrer une double inclusion ? pcq dans le corrigé d'un exercice il ne l'ont pas fait

Bonjour C'est tout de même pas la mer à boire!!! On suppose que a,b>0 et que a\neq b. Alors a/(1+b)-b/(1+a)=....... continue, il y en a pour 30s. On aurait aimé voir le raisonnement par l'absurde. pour le raisonnement par l'absurde on suppose que a/(1+b)= b/(1+a) et a est différent de b on aura par...

pour a>=0 et b>=0 montrer que a/(1+b) =b/(1+a) implique que a = b

j'ai réussi a la démontrer par l'absurde mais l'exercice demande de le faire par la contraposée

la fonction racine carree de X est elle continue sur R*+ ou R+ ?

rcompany a écrit:As-tu essayé d’appliquer la règle de l’Hopital?

l'exercice dit qu'il faut la calculer sans la régle de l'hopital

calculer la limite suivante
sin(picos(x))/xsin(x) quand x tend vers 0 .

ps: l'editeur d'equation ne marche pas chez moi je sais pas pq

soit B: ∀x,y ∈ R ,((x>0) et (y>0) ⇒ xy>0) montrer que B⇒A

donner la negation de la proposition suivante: ∀x∈R, (x>0 ⇒(1/x) >0)

merci!

soit n dans N* montrer que (n²+1)^(1/2) n'est pas un entier

montrer que ∀n∊N la somme de k=0 jusqu'a k=n de K² est egale a n(n+1)(2n+1)/6 puis en deduire la somme de k=0 jusqu'a k=n de K^3
pour la premiere question je m'en sort mais pour la 2eme je suis pas si sur

Bonjour C'est FAUX! 1+(1/2)>1 Bonjour mimosa, Ici c'est le quantificateur "quel que soit" qui est important. Récris en latex, il faut montrer que \forall x\in\R,\forall n\in\N^\star, x<1+\dfrac{1}{n}\Rightarrow x\leq 1 @haitem6 : Si x est inférieur à 1+1/2, à 1+1/3, à 1+1/4, etc., peut-il...

montrer que ∀x dans R,∀n dans N* (x <1 + (1/n) ⇒ x<= 1)

d'accord merci.
bonne journee

Ben314 a écrit:Salut,
, par définition, ça signifie .
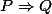
C'est quoi la négation de de ? de ? de ?

j'ai pas compris

c quoi la negation d'une equivalence , genre la negation de P ⇔ Q

qlqn peut me rappeler l'axiome d'archimede svp

montrer que a= ∛(20+14√2) + ∛(20-14√2) est un entier (on utilise (a+b)^3 mais je bloque )