Merci beaucoup
LB2 , l’anneau présenterait une loi d’addition (f+g)(x)=f(x)+g(x) et une loi multiplicative (fg)(x)=f(x)g(x) qui respecte les axiomes
25 résultats trouvés
Revenir à la recherche avancée
Structure
Bonjour j’aimerais savoir si la réponse suivante est juste?A de type S ssi pour tous (z_{1},z_{2}) appartenant à A on a z_{1}z_{2} et z_{1}^2+z_{2}^2 appartenant à A Soit /A ={[/z,z appartenant à A Mq /A est de type S Soit A munis de la structure S et /: A dans /A et qui à z associe /z on a...
Anneaux
Bonjour je me demandais si l'assertion suivante est vraie?
Soit) un anneaux et E un ensemble quelconque, s'il existe un isomorphisme de l'anneaux dans E alors E est un anneaux
un anneaux et E un ensemble quelconque, s'il existe un isomorphisme de l'anneaux dans E alors E est un anneaux )
Soit
Re: modules des solutions d’une équation du second degré
Ok merci beaucoup
- 21 Jan 2019, 17:34
- Forum: ✎✎ Lycée
- Sujet: modules des solutions d’une équation du second degré
- Réponses: 4
- Vues: 630
Re: modules des solutions d’une équation du second degré
Merci, mais c’est la question 2 qui me posait problème, je n’ai aucune piste pour déterminer la condition nécessaire et suffisante
- 21 Jan 2019, 12:02
- Forum: ✎✎ Lycée
- Sujet: modules des solutions d’une équation du second degré
- Réponses: 4
- Vues: 630
modules des solutions d’une équation du second degré
Bonjour, Je n’arrive pas à résoudre la question 2 de l’exo Dont l’énoncé est ci dessous, Soient (z_{1},z_{2}) les solutions de l’equation z^{2}+nz+m=0, (n,m) de C\times C* 1) écrire une équation à l’aide de n et de m dont les solutions sont u_{1}=z_{1}/z_{2} et u_{2}=z_{2}/z_{1} 2) d...
- 21 Jan 2019, 00:47
- Forum: ✎✎ Lycée
- Sujet: modules des solutions d’une équation du second degré
- Réponses: 4
- Vues: 630
Re: Codage affine
En fait mon problème est différent, je me suis sûrement mal exprimé, le problème étant de trouvé tous les a qui fonctionnent ou démontrer que cette congruences est fausse
- 03 Déc 2018, 19:34
- Forum: ✎✎ Lycée
- Sujet: Codage affine
- Réponses: 2
- Vues: 380
Codage affine
Bonjour,
Je me demandais si un codage modélisé par la congruence était possible?
était possible?
Je pensais a démontré que cela est impossible à l'aide de propriété dans les congruences mais je ne suis pas sûr ?
Je me demandais si un codage modélisé par la congruence
Je pensais a démontré que cela est impossible à l'aide de propriété dans les congruences mais je ne suis pas sûr ?
- 03 Déc 2018, 17:53
- Forum: ✎✎ Lycée
- Sujet: Codage affine
- Réponses: 2
- Vues: 380
Re: Limite
Ok merci
Re: Limite
Et par la même occasion si 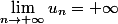 et suffisant pour dire q'une suite diverge
et suffisant pour dire q'une suite diverge
Limite
Bonjour j'aimerais savoir si 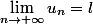 est suffisant pour dire qu'une suite converge
est suffisant pour dire qu'une suite converge
Re: Congruences dans Z
Merci
- 04 Oct 2018, 11:17
- Forum: ✎✎ Lycée
- Sujet: Congruences dans Z
- Réponses: 5
- Vues: 540
Congruences dans Z
Voilà, j'aimerais savoir si mon raisonnement est juste où pas, ( déterminer le reste de 91234^2002) 91234\equiv 3[7]\Rightarrow 91234^{2002}\equiv 3^{2002}\equiv (3^{2})^{1001}\equiv 2^{1001}\equiv 2^{3\times 333}\times 2^{2}\equiv 4[7] , ou s'il existe un meilleur moyen de résoudre ce probl...
- 03 Oct 2018, 15:08
- Forum: ✎✎ Lycée
- Sujet: Congruences dans Z
- Réponses: 5
- Vues: 540
Re: Équation complexe
Merci beaucoup, ca paraît logique maintenant 
- 26 Sep 2018, 19:16
- Forum: ✎✎ Lycée
- Sujet: Équation complexe
- Réponses: 4
- Vues: 192
Équation complexe
Bonjour, je n'arrive pas à résoudre ^{2}=0) , j'aimerai donc connaître une méthode pour la résoudre, s'il vous plaît.
, j'aimerai donc connaître une méthode pour la résoudre, s'il vous plaît.
Merci
Merci
- 26 Sep 2018, 18:52
- Forum: ✎✎ Lycée
- Sujet: Équation complexe
- Réponses: 4
- Vues: 192
Re: Diviseur
Merci pour ton aide
Diviseur
Bonjour, je dois montrer que pour a et b deux entiers naturels tels que 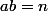 avec
avec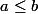 , on a
, on a 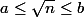
Je ne sais pas comment m'y prendre.
Merci
Je ne sais pas comment m'y prendre.
Merci
Re: potentiel vecteur et champ scalaire
Ok merci pour ton aide
- 28 Aoû 2018, 21:11
- Forum: ⚛ Physique
- Sujet: potentiel vecteur et champ scalaire
- Réponses: 6
- Vues: 591
Re: potentiel vecteur et champ scalaire
Alors question qui peut sembler bête mais peut on inscrire un champ scalaire a l'aide de ses composantes en x,y,z.
Sinon je ne comprends pas la suite des calculs à faire pour arriver s=...
Sinon je ne comprends pas la suite des calculs à faire pour arriver s=...
- 28 Aoû 2018, 20:05
- Forum: ⚛ Physique
- Sujet: potentiel vecteur et champ scalaire
- Réponses: 6
- Vues: 591
Re: potentiel vecteur et champ scalaire
Excuse moi, mais que signifie ) , est-ce une constante? Si je suis ce raisonnement
, est-ce une constante? Si je suis ce raisonnement 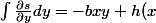)
- 28 Aoû 2018, 18:55
- Forum: ⚛ Physique
- Sujet: potentiel vecteur et champ scalaire
- Réponses: 6
- Vues: 591
- 25 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
