D'accord,
Je vous remercie tous pour votre aide
45 résultats trouvés
Revenir à la recherche avancée
- 22 Aoû 2018, 08:50
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
D'accord merci
J'aurais juste une dernière petite question à vous poser.
Si on veut calculer une valeur numérique de f(1) par exemple, est-ce qu'il faut mettre la calculatrice en degré ou en radian pour avoir une valeur approchée?
J'aurais juste une dernière petite question à vous poser.
Si on veut calculer une valeur numérique de f(1) par exemple, est-ce qu'il faut mettre la calculatrice en degré ou en radian pour avoir une valeur approchée?
- 22 Aoû 2018, 08:16
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Suite de polynôme
Oui mais je ne sais pas comment aboutir à ça, j'ai mes deux solutions particulière de l’équation caractéristique mais après je ne vois pas comment faire
- 22 Aoû 2018, 08:15
- Forum: ✯✎ Supérieur
- Sujet: Suite de polynôme
- Réponses: 22
- Vues: 527
Re: Suite de polynôme
D'accord merci
Avez vous une indication pour la question h)?
Avez vous une indication pour la question h)?
- 21 Aoû 2018, 22:13
- Forum: ✯✎ Supérieur
- Sujet: Suite de polynôme
- Réponses: 22
- Vues: 527
Re: Polynomes
Oui oui mais ce que je veux dire c'est qu'il faut remplacer les Pn et Qn aussi non? Pour avoir juste des a_0, a_1, ..., a_n
- 21 Aoû 2018, 22:10
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
Ah oui pardon mais je ne comprends pas comment on peut passer de f et f' à f^(n+1)(x)
- 21 Aoû 2018, 20:08
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
Est-ce que c'est ça le développement limité?
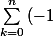^{2k+1}\frac{x^k}{2(2k+1)!}}+o(x^n)) ?
?
- 21 Aoû 2018, 19:06
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Suite de polynôme
Oui je suis d'accord mais je ne comprends pas comment on peut en déduire les égalités demandées... Parce que  =1 = (-1)^0) donc c'est vérifié pour n=0 mais ça veut pas dire que c'est valable pour tous les n, si?
donc c'est vérifié pour n=0 mais ça veut pas dire que c'est valable pour tous les n, si?
- 21 Aoû 2018, 15:49
- Forum: ✯✎ Supérieur
- Sujet: Suite de polynôme
- Réponses: 22
- Vues: 527
Re: Polynomes
d'accord merci beaucoup Il y a une dernière question que j'ai oublié d'écrire dans le premier message: Montrer que f et f' admettent des développements limités à tout ordre en 0. Conclure qu'il existe des réels a_0, a_1, ..., a_n tels que: f^{(n+1)}(x) = \frac{a_0}{x^n}+\frac{a_1}{x^...
- 21 Aoû 2018, 15:26
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
D'accord merci et pour trouver une relation entre P_n+1, P_n, Q_n+1 et Q_n, comment peut-on éliminer les P' et Q'?
- 21 Aoû 2018, 13:50
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
J'ai obtenu cette équation: x^{n+1}f^{(n+2)}(x) = f(x)[xP'_n(x)+Q_n(x)P_1(x)-nP_n(x)] +f'(x)[xP_n(x)+xQ'_n(x)+Q_n(x)Q_1(x)-nQ_n(x)] Du coup les parties entre crochets seraient P_{n+1} ...
- 21 Aoû 2018, 13:33
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
D'accord merci! Pour la g), j'ai fait dérivé donc j'ai ça: nx^{n-1}f^{(n+1)}(x) +x^{n}f^{(n+2)}(x) = P'_n(x)f(x)+P_n(x)f'(x)+Q'_n(x)f'(x)+Q_n(x)f''(x) Le problème c'est que je ne p...
- 21 Aoû 2018, 13:13
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
D'accord je vais essayer comme vous avez dit.
Est-ce que la f) vous semble juste?
Est-ce que la f) vous semble juste?
- 21 Aoû 2018, 12:48
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
J'ai refait mon calcul et j'ai trouvé:
P1(x) =-1/4 et Q1(x) = -1/2
Pour la g), je me doute que c'est une récurrence mais comme je l'ai dit, je bloque sur l'hérédité, je n'arrive pas à trouver comment faire
P1(x) =-1/4 et Q1(x) = -1/2
Pour la g), je me doute que c'est une récurrence mais comme je l'ai dit, je bloque sur l'hérédité, je n'arrive pas à trouver comment faire
- 21 Aoû 2018, 12:27
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
D'accord merci,
Pourrais-je avoir une indication de la part de quelqu'un pour la question g) à présent?
Pourrais-je avoir une indication de la part de quelqu'un pour la question g) à présent?
- 21 Aoû 2018, 10:51
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
Donc j'ai ça:
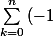^{k} * \frac{x^{k}}{(2k)!}} +o(x^{k})) ?
?
du coup f admet un développement limité à tout ordre en 0?
du coup f admet un développement limité à tout ordre en 0?
- 21 Aoû 2018, 10:45
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
Comment ça l'arranger?
- 21 Aoû 2018, 10:40
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
Est-ce que quelqu'un pourrait répondre à ma question s'il vous plait?
- 21 Aoû 2018, 10:32
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
Est-ce qu'on peut dire que vu que f s'écrit sous la forme d'une somme allant jusqu’au rang n, f admet un DL à tout ordre?
- 21 Aoû 2018, 09:36
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
Re: Polynomes
Donc on a:
f(x) =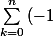^{k}*\frac{\sqrt{x}^{2k}}{(2k)!}} + o(\sqrt{x}^{2k})) ?
?
f(x) =
- 21 Aoû 2018, 08:16
- Forum: ✯✎ Supérieur
- Sujet: Polynomes
- Réponses: 75
- Vues: 1338
- 45 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
