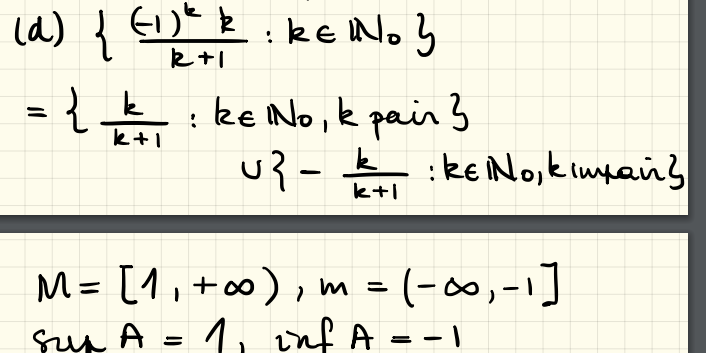113 résultats trouvés
Revenir à la recherche avancée
Re: Question sur les majorants
Merci catamat
- 03 Mar 2025, 21:20
- Forum: ✎✎ Lycée
- Sujet: Question sur les majorants
- Réponses: 8
- Vues: 5769
Re: Question sur les majorants
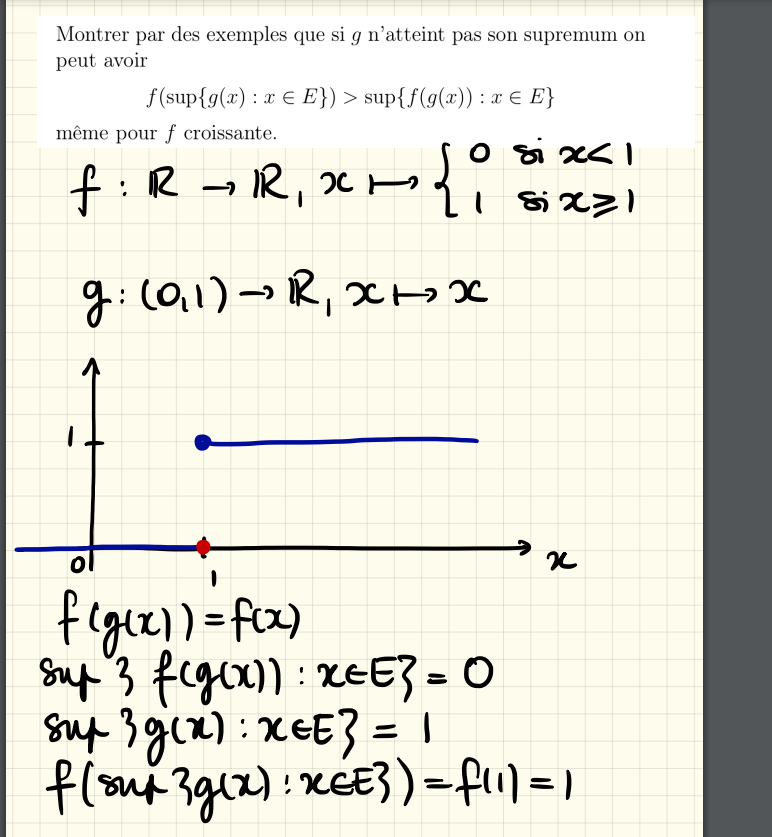
Dans le même thème, pourrais-t-on m'expliquer pourquoi le supremum de f°g est 0, question toute bête mais qui m'échappe ...

- 02 Mar 2025, 11:16
- Forum: ✎✎ Lycée
- Sujet: Question sur les majorants
- Réponses: 8
- Vues: 5769
Re: Question sur les majorants
Merci Ben et catamat !
- 23 Fév 2025, 18:27
- Forum: ✎✎ Lycée
- Sujet: Question sur les majorants
- Réponses: 8
- Vues: 5769
- 23 Fév 2025, 10:36
- Forum: ✎✎ Lycée
- Sujet: Question sur les majorants
- Réponses: 8
- Vues: 5769
Re: Question sur les majorants
C'était exactement mon raisonnement mais dans le correctif l'assistante a suggéré comme ensemble des majorants l'ensemble [1,+inf[, je poste ici plus bas la photo du correctif, serait-ce une malencontreuse erreur ou j'ai mal interpreté quelque chose? https://image.noelshack.com/fichiers/2025/08/7/17...
- 23 Fév 2025, 10:34
- Forum: ✎✎ Lycée
- Sujet: Question sur les majorants
- Réponses: 8
- Vues: 5769
Question sur les majorants
Bonjour, pour le c) et le d) je ne comprends pas pourquoi pour cette ensemble on parle de majorants supérieurs à 1 puisqu'il est défini avec K appartenant à N sauf 0 il ne devrait pas y avoir de majorant supérieur à 1 ou ai-je mal compris quelque chose ? https://image.noelshack.com/fichiers/2025/08/...
- 22 Fév 2025, 14:13
- Forum: ✎✎ Lycée
- Sujet: Question sur les majorants
- Réponses: 8
- Vues: 5769
Re: Intersection de familles d'ensembles
Bonjour à tous J'ai un imprévu , je ne peux pas suivre l'échange davantage, j'espère qu'un autre membre sera plus disponible @mythostyle : en bref (à rédiger mieux, à détailler) l'intersection des Ak pour k de 1 à n est An lui même , donc cette intersection est non vide. il n'existe aucun réel qui ...
- 19 Fév 2025, 18:56
- Forum: ✯✎ Supérieur
- Sujet: Intersection de familles d'ensembles
- Réponses: 6
- Vues: 1650
Re: Intersection de familles d'ensembles
Merci à vous deux, en particulier je dois me repencher sur les explications de Ben par des exemples car je saisis à moitié, mais si je comprends bien la réponse est familièrement formulée comme suit : Pour un nombre n donné les intersections de An pour la suite ]0,1/k] est non-vide mais l'intersecti...
- 19 Fév 2025, 03:13
- Forum: ✯✎ Supérieur
- Sujet: Intersection de familles d'ensembles
- Réponses: 6
- Vues: 1650
Intersection de familles d'ensembles
Bonjour, j'ai du mal à concevoir pourquoi cette affirmation est fausse et donc à trouver un contre exemple help 
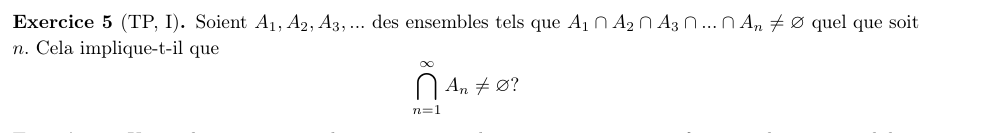
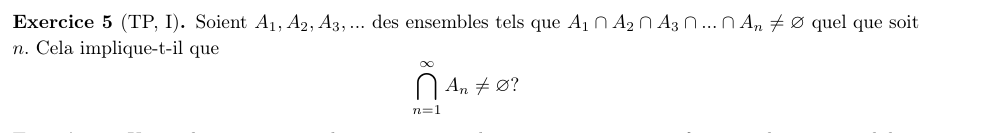
- 18 Fév 2025, 15:51
- Forum: ✯✎ Supérieur
- Sujet: Intersection de familles d'ensembles
- Réponses: 6
- Vues: 1650
Re: dérivée d'une fonction composée
Non je ne connaissais pas, super c'est exactement ce que je cherchais, merci !
- 16 Fév 2025, 23:24
- Forum: ✎✎ Lycée
- Sujet: dérivée d'une fonction composée
- Réponses: 11
- Vues: 5959
Re: dérivée d'une fonction composée
Merci Ben !
à ce sujet quelqu'un qui passerait par ici par hasard aurait-il un lien vers des exercices corrigés d'expressions à dériver/intégrer pour que je m'entraîne je trouve que le syllabus du cours n'est pas très fourni
à ce sujet quelqu'un qui passerait par ici par hasard aurait-il un lien vers des exercices corrigés d'expressions à dériver/intégrer pour que je m'entraîne je trouve que le syllabus du cours n'est pas très fourni
- 16 Fév 2025, 11:27
- Forum: ✎✎ Lycée
- Sujet: dérivée d'une fonction composée
- Réponses: 11
- Vues: 5959
Re: dérivée d'une fonction composée
De nouveau pour ne pas polluer le forum je pose ça ici, je cherche la primitive de 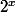 après avoir fait une belle gaffe j'ai vu que la réponse est
après avoir fait une belle gaffe j'ai vu que la réponse est ) mais je ne comprends pas comment on est parvenu à ce résultat
mais je ne comprends pas comment on est parvenu à ce résultat
- 15 Fév 2025, 19:20
- Forum: ✎✎ Lycée
- Sujet: dérivée d'une fonction composée
- Réponses: 11
- Vues: 5959
Re: dérivée d'une fonction composée
Merci à vous deux !
- 13 Fév 2025, 10:44
- Forum: ✎✎ Lycée
- Sujet: dérivée d'une fonction composée
- Réponses: 11
- Vues: 5959
Re: dérivée d'une fonction composée
Personnellement j'ai directement dérivée dy/dx mais ils semblent être arrivé à la solution grâce à une suite de calculs intermédiaires que je ne connais pas
- 12 Fév 2025, 14:30
- Forum: ✎✎ Lycée
- Sujet: dérivée d'une fonction composée
- Réponses: 11
- Vues: 5959
dérivée d'une fonction composée
Bonjour à tous, j'essaie de comprendre la méthode très intéressante qui a été utilisée ici pour dérivée une fonction composée mais j'ai du mal à comprendre quelqu'un saurait m'éclairer ? https://image.noelshack.com/fichiers/2025/07/3/1739366732-correc-1.png https://image.noelshack.com/fichiers/2025/...
- 12 Fév 2025, 14:26
- Forum: ✎✎ Lycée
- Sujet: dérivée d'une fonction composée
- Réponses: 11
- Vues: 5959
Re: Equation complexe
Afin de ne pas polluer le forum j ai une autre toute petite question sans rapport avec les complexes je prends l’initiative de la poster ici en espérant qu’elle sera prise en compte. Quelles pistes puis-je utiliser pour demontrer la consequence des axiomes d ordre total énoncé dans le dernier paragr...
- 31 Déc 2024, 19:07
- Forum: ✎✎ Lycée
- Sujet: Equation complexe
- Réponses: 5
- Vues: 5424
Re: Equation complexe
merci vam !
- 30 Déc 2024, 17:30
- Forum: ✎✎ Lycée
- Sujet: Equation complexe
- Réponses: 5
- Vues: 5424
Equation complexe
Bonjour j ai du mal à résoudre l exercice 7 c lorsque je calcule le discriminant reduit je tombe sur -3 + 4i et lorsque je veux calculer la racine de celui ci lors du passage en forme polaire je tombe sur des approximations qui m’eloigne de la solution du syllabus quelqu’un pourrait il m’eclairer? h...
- 29 Déc 2024, 15:55
- Forum: ✎✎ Lycée
- Sujet: Equation complexe
- Réponses: 5
- Vues: 5424
Re: Fonction continue en un point
Merci catamat !
- 17 Déc 2024, 21:21
- Forum: ✎✎ Lycée
- Sujet: Fonction continue en un point
- Réponses: 2
- Vues: 3461
Fonction continue en un point
Bonjour !
Comment à partir de cet énoncé je suis capable de dire que u(x) est continue en a ? Il s’agit de l hypothèse utilisée dans le correctif pour justifier=u(a)\])
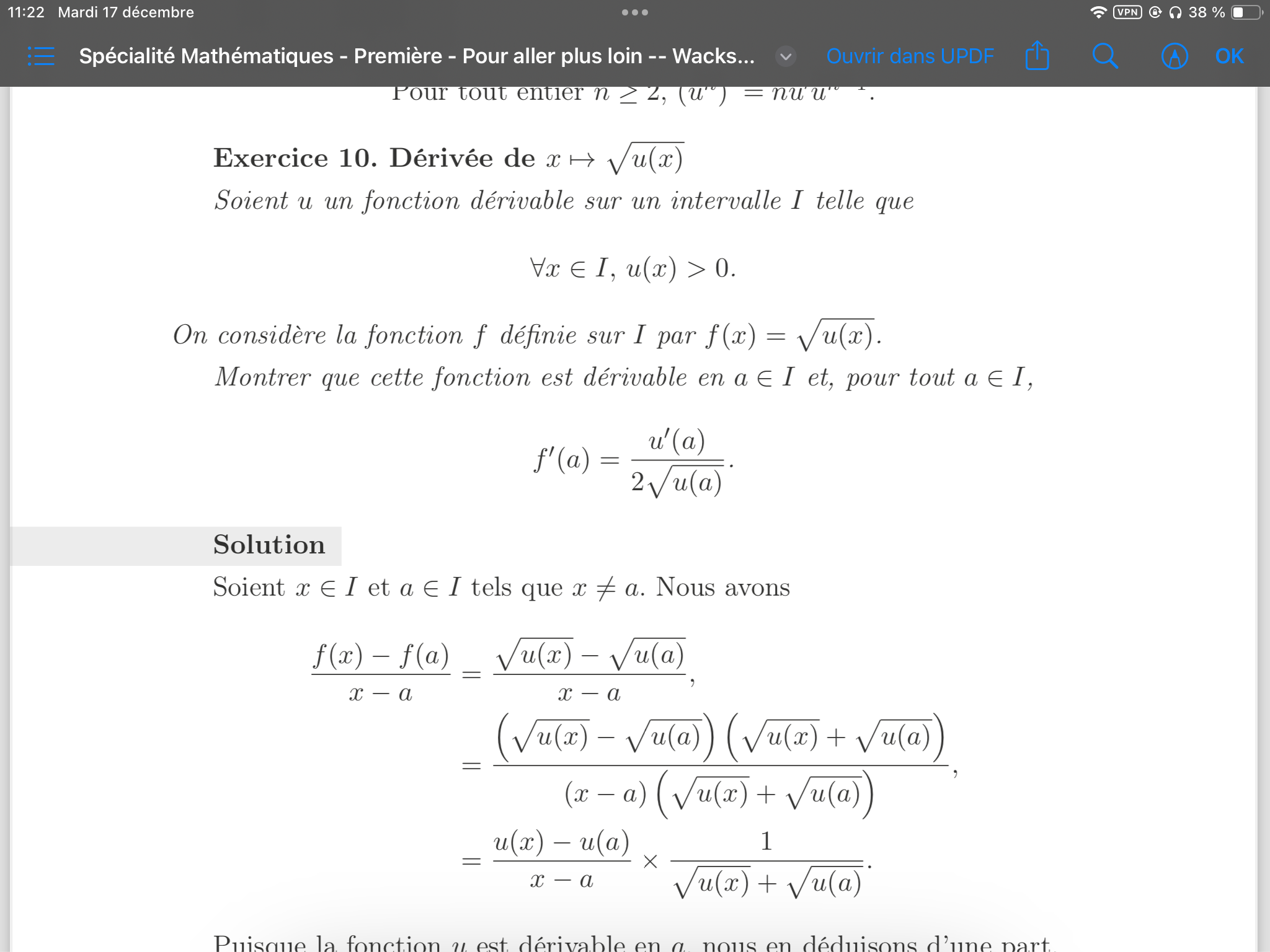
Comment à partir de cet énoncé je suis capable de dire que u(x) est continue en a ? Il s’agit de l hypothèse utilisée dans le correctif pour justifier

- 17 Déc 2024, 11:28
- Forum: ✎✎ Lycée
- Sujet: Fonction continue en un point
- Réponses: 2
- Vues: 3461
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :