11 résultats trouvés
Revenir à la recherche avancée
Re: Borne supérieure sur système linéaire de Vandermonde
Malheureusement les \alpha_i ne sont pas uniformèment distribués. En fait ils correspondent aux noeuds de Legendre-Gauss-Lobatto. Plus précisément si \{x_i\}_{i=1}^s \subset [-1,1] sont les noeuds, pour un r \in \{x_i\}_{i=1}^s je réécris x_i = r + 2\alpha_i et donc j'ai bien 0 \leq |\alpha_i |\leq ...
- 02 Juin 2020, 12:12
- Forum: ✯✎ Supérieur
- Sujet: Borne supérieure sur système linéaire de Vandermonde
- Réponses: 10
- Vues: 645
Re: Borne supérieure sur système linéaire de Vandermonde
Mince, je me suis trompé, en fait j'avais : \Large\Delta_\alpha^{\frac{s}{2}(s-1)} Si V est la matrice de Vandermonde, par définition de \Delta_\alpha on obtient \Large|det(V)| \ge \prod_{1\leq i < j \leq s} \Delta_\alpha . Et 1\leq i < j \leq s correspond au nombre d'éléments d'une ...
- 02 Juin 2020, 09:56
- Forum: ✯✎ Supérieur
- Sujet: Borne supérieure sur système linéaire de Vandermonde
- Réponses: 10
- Vues: 645
Re: Borne supérieure sur système linéaire de Vandermonde
Désolé, je n'avais pas vu ton message.
J'ai obtenu la borne}}) , où
, où 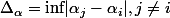 .
.
J'ai obtenu la borne
- 01 Juin 2020, 17:20
- Forum: ✯✎ Supérieur
- Sujet: Borne supérieure sur système linéaire de Vandermonde
- Réponses: 10
- Vues: 645
Re: Borne supérieure sur système linéaire de Vandermonde
Bonjour,
Merci pour ta réponse, je pense avoir trouvé une borne maintenant. Et aussi merci pour l'astuce !
Merci pour ta réponse, je pense avoir trouvé une borne maintenant. Et aussi merci pour l'astuce !
- 28 Mai 2020, 17:17
- Forum: ✯✎ Supérieur
- Sujet: Borne supérieure sur système linéaire de Vandermonde
- Réponses: 10
- Vues: 645
Borne supérieure sur système linéaire de Vandermonde
Bonjour, Pour un code sur Matlab, j'utilise le système ci-dessous pour calculer les coefficients d'une méthode des différences finies. Cependant, pour prouver que la méthode converge, je dois prouver que \sum_{i=1}^s |a_i| est borné supérieurement. Sachant que -1\leq\alpha_i\leq1 , et que mes expéri...
- 28 Mai 2020, 11:11
- Forum: ✯✎ Supérieur
- Sujet: Borne supérieure sur système linéaire de Vandermonde
- Réponses: 10
- Vues: 645
Re: Groupes et isomorphismes
Et [G,G] le sous groupe dérivé de G :

- 26 Nov 2018, 21:16
- Forum: ✯✎ Supérieur
- Sujet: Groupes et isomorphismes
- Réponses: 4
- Vues: 331
Re: Groupes et isomorphismes
Pour moi c'est le normalisateur de  dans
dans  :
:  = \{g \in G : gHg^{-1} = H\})
- 26 Nov 2018, 21:14
- Forum: ✯✎ Supérieur
- Sujet: Groupes et isomorphismes
- Réponses: 4
- Vues: 331
Groupes et isomorphismes
Bonjour, Il y a une question à laquelle je n'arrive pas à répondre : Sachant que G est un groupe d'ordre 55 et qu'il possède 2 sous-groupes : - H de cardinal 5 avec N_{G}(H) = H . - N de cardinal 11 avec N normal dans G . Montrer que G est isomorphe à un sous-groupe de S_{11} . J'ai montré d...
- 26 Nov 2018, 21:04
- Forum: ✯✎ Supérieur
- Sujet: Groupes et isomorphismes
- Réponses: 4
- Vues: 331
Re: Isomorphisme d'anneaux
Oui sinon pas de théorème d'isomorphisme encore merci !
- 15 Mai 2018, 13:17
- Forum: ✯✎ Supérieur
- Sujet: Isomorphisme d'anneaux
- Réponses: 5
- Vues: 383
Re: Isomorphisme d'anneaux
Salut, D'abord oui effectivement il ne devrait pas y avoir de i ! Merci beaucoup pour vos réponses je crois que j'ai finalement réussi à résoudre cet exercice : si on prend le morphisme d'évaluation \phi : f(x,y) -> (f(x,1), f(-1,y)) on a bien P(-1) = Q(1), et il n'y ...
- 14 Mai 2018, 15:16
- Forum: ✯✎ Supérieur
- Sujet: Isomorphisme d'anneaux
- Réponses: 5
- Vues: 383
Isomorphisme d'anneaux
Bonjour, Je suis bloqué sur un exercice dans lequel je dois prouver que l’anneau quotient C[x, y]/<(x+1)(y−1)i> est isomorphe au sous-anneau de C[x] × C[y] des paires de polynômes (P(x), Q(y)) tel que P(−1) = Q(1). J'ai d'abord pensé utiliser le premier théorème d'isomorphisme en prenant phi : C[x,y...
- 13 Mai 2018, 14:00
- Forum: ✯✎ Supérieur
- Sujet: Isomorphisme d'anneaux
- Réponses: 5
- Vues: 383
- 11 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
