Forum de Mathématiques: Maths-Forum

Bonjour, J'ai envoyé il y a peu une demande d'autorisation d'enseigner au rectorat. Naïvement, dans l'encart "diplomes obtenus" je note "licence de mathématiques" comme d'habitude. Sauf que cette fois-ci le document m'a été retourné en m'expliquant que l'information ne correspond...

Bonjour à tous. Je reviens tout droit de chez le coiffeur; c'est toujours sympa de discuter avec lui parceque c'est le roi des astuces mathématiques pour calculer les concentrations. Mais ce coup-ci il m'a collé: Il m'a dit qu'il connaissait une astuce appelée la "croix de Saint André" mais qu'il ét...

Ce sont les fonctions localement integrables ou integrables sur tout compact.
Autrement dit quelque soit un compact K, l'integrale d'une telle fonction sur K est bien définie, c'est à dire finie.

A mon avis il faut discuter de la parité en fonction de l'ensemble considéré. Si l'ensemble est donné ça risque d'être trivial...

je crois que c'est plutot
sinon je ne vois pas trop comment prouver quoi que ce soit...

bonne nuit!
faudra revenir nous parler de la correction :ptdr:

argsh(x) = ln(x + \sqrt{x^2 +1 })\ , Si tu as bien compris, ça c'est l'inverse (pour l'opération o) de sh. C'est à dire que (shx)o(argshx)=x. Donc si E était un groupe pour la loi o, ch devrait avoir aussi un inverse (c'est la base d'un groupe) or ch n'en a pas puisqu'il n'est pas b...

En fait j'ai la preuve que ça ne marche pas.
E ne peut pas avoir de structure de groupe pour la composition puisque ch(x) qui appartient à E n'a pas de fonction réciproque !!

Ben en fait je me suis rappelé des vieux vieux souvenirs: E est en fait l'ensemble des fonction C^\infty\ et comme en composant deux fonctions C^\infty\ on a une fonction C^\infty\ , la composée peut s'ecrire ae^x+be^{-x} . Le problème c'est de retrouver les a et b qui conviennent! Je suis en train ...

tu connais les fonctions hyperboliques sh et ch?

Soit il y a erreur d'énoncé, soit on interprete mal...

Y avait-il des question avant sur le même exercice?

Tu cherches quel genre de morphisme? un morphisme de groupe? une application linéaire?

n'as tu pas confondu (E,o) avec (E,+)?

Tu as directement recopier le sujet depuis ta feuille ou tu nous le ressors de tête?

C'est tout le problème en fait... J'ai répondu un peu vite parceque j'ai déjà vu cet exercice et c'est vrai que cette réponse colle pas trop à ton énoncé. Mais je vois pas trop comment y arriver en utilisant la composition classique. Essaye de voir avec une calculatrice si tu as une égalité pour que...

en fait la quuestion est tres tordue (Fp)o(Fq)(x)= (Fp)[f(x+q)]=f((x+q)+p)=f(x+q+p)=Fp+q(x) Ne pas confondre les Fp avec les f!!! En relisant l'énnoncé c'est vrai que ma réponse colle pas trop, mais c'est comme ça que je connais cet exercice ensuite un morphisme bijectif s'appelle un isomorphisme à ...

Effectivement, ce que tu viens de completer est juste. Je ne connaissait pas ce résultat mais je l'ai trouvé ici http://www.u-cergy.fr/rech/pages/courilleau/Sources/cours06_07/SobolevN.pdf Quand on réussi à faire le tri dans les notations et que l'on retrouve ton cas particulier, ils expliquent à pe...

Justement, dans mes références, je n'ai jamais vu H^1_0 écrit comme ça. Quand je disais que je comprenais très bien de quoi tu parlais, c'est justement car je sais aussi qu'en gros dans H^1_0 on parle de fonctions qui s'annulent au bord. Mais c'est justement le "en gros" qui nous pose prob...

oui c'est ça.
Par contre comme yos a le même problème que moi pour trouver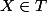 regarde si tu ne t'es pas trompé sur ton énnoncé.
est-ce bien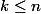 et pas l'inverse?
n'as tu pas directement oublié directement N dans la définition de T?

En fait j'ai aussi un problème pour voir que N tout entier est ouvert, sinon pour le reste 1) l'ensemble vide est dans T (c'est écrit d'ssus) 2) une réunion (même) infinie d'ouvert est un ouvert regarde un peu la réunion de seulement 2 ouverts et tu verras comment simplifier l'affaire. Le seul probl...

Pardon je n'avais pas vu la première question:
en fait les ouverts, c'est à dire les élément de T doivent vérifié certaines propriétés, si mes souvenirs sont bons on doit montrer par exemple que l'intersection de deux elements de T reste dans T et quelques autre propriétés dans le genre

Si T c'est bien ta définition des ouverts,
les fermés sont les complémentaires des ouverts, donc cherche les complémentaires des ouverts U de T.