Forum de Mathématiques: Maths-Forum

Bonjour, je me permets de partager une question : Soient A,~B,~C,~D des groupes tels que C\triangleleft A, A\triangleleft B et C\triangleleft D,~ D \triangleleft B . A-t-on alors : \dfrac{B}{A}\simeq\dfrac{D}{C} \Longrightarrow \dfrac{B}{D}\simeq\dfrac{A}{C} ? En claire, j'ai remarqué au cours d'un ...

tout à fait ! ^^ j'aurais aimé y penser..
Je n'en voyais pas le bout et surtout je n'arrivais pas a avancer

En tous cas je te remercie vraiment ! :p

oui évidemment ! ^^ merci Bon, j'ai fini mon DM en laissant un blanc... Je ne comprends pas comment faire cette récurrence.. pour le moment j'ai: P_n : "\forall n \in \mathbb{N}, |h^n(z)-z_0|<(\frac{1}{\pi})^n|z-z_0|" Initialisation : |h(z)-h(z_0)|< \frac{1}...

pourquoi ? enfin, je veux dire, à moins que 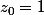, je ne comprends pas comment affirmer ça

Merci Black Jack j'ai corrigé ;) par contre ta méthode à beau me plaire (j'y avais pensé), je ne pense pas qu'elle convienne vraiment ... Il faut "en conclure" une methode à partir de la question précédente. Et sinon, je te remercie aussi raito123, je vais essayer de montrer tout ca, je re...

Merci raito123 ! :D Sans me donner la réponse tu as su m'aider, ça fait toujours plaisir Edit: par contre je veux bien un peu d'aide pour la g) ^^ je vois bien qu'il faut utiliser le théorème du point fixe... Mais sans calculatrice je ne comprends pas comment donner une valeur approchée plus précise...

Bonjour, alors voilà, je voudrais bien un peu d'aide, j'ai beau chercher, je ne vois pas comment faire cette démonstration: on etudie la fonction $f(x)=|x|^{\frac{\pi}{4}}$ . sin(x) J'ai pu montrer qu'elle était impaire sur \mathbb{R} , qu'elle diverge en + et - infini, qu'elle est dérivable...

Merci pascal16,
j'essaie de faire comme ça (peut être que j'ai essayé de faire trop 'fin' jusque là ^^)

edit: merci pour votre aide, j'ai enfin réussi

Merci chan79 !
je vais essayer ça, même si je ne suis pas sûr de vraiment savoir où m'en servir

edit: effectivement je ne vois pas comment faire... merci quand même

Bonjour, je vous présente l'énoncé: On considère les suites $(u_n)_{n\geq 0} et $(v_n)_{n\geq 0}$ définies par : u_0 = 0, v_0=0, \forall n \in \mathbb{N}, u_{n+1}=\sqrt{3-v_n}, v_{n+1}=\sqrt{ 3 +u_n} 1) Justifier que ces suites sont bien définies. 2) Démontrer que, $\forall n \in \ma...