Forum de Mathématiques: Maths-Forum

ah!!! oui ok merci!!!

ou si j'ai pas compris..

merci de ta réponse,
il y a que 6+4i qui convient mais ça ne marche pas dans l'équation...si je ne m'abuse

Bonjour, J'ai une première équation qui est z^2+2iz-5=0 Je trouve 2-i en solution Normalement c'est bon Mais le problème c'est que j'ai une autre question qui ressemble z^2+2(1+i)z-5(1+2i)=0 La par contre je trouve pas,j'essaie la méthode précédente en passant par le discriminant \De...

argh effectivement..ok merci !!

Bonjour!
Pourriez vous juste me confirmer que la primitive de 1/(1+2x^2) est bien



J'ai un doute avec le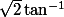 quand je le dérive à l'inverse....

Merci bien!

yes merci!

Bonjour,que de problèmes et de difficultés E: x''(t)-4x'(t)=e(4t) Déterminer la soluce générale de E=0 Alors j'ai r1=4 et r2=0 Donc De(4x) +E Déterminer une soluce particulière de E sous la forme x(t)=(at+b)e(4t) donc je détermine les x'(t) et x''(t) ae(4t)+(4at)e(4t)+(4b)e(4t) e(4t)+(4a)e(4t)+(4a)e...

merci je n'avais pas fais le lien avec le module

ok,du coup je remplace (x+yi)^2 par ce que tu trouve précédemment et je dois trouver -3-2j
J'essaie merci

oui j'ai remarqué ça, mais je n'arrive pas à aller plus loin...
pardon j'avais pas vu la suite

Bonjour,je suis de nouveau bloqué sur une équation z^{2}=-3-2i J'essai en faisant (x+yi)^2=-3-2i Ducoup x^2-y^2=-3 x*y=-1 Je trouve y =2 et x=-0.5 soit (-0.5+2i) et en faisant avec le module ou en changeant de forme je n'y arrive pas non plus.. Mais quand je reprend l’équation j'ai pas le bon résult...

argh nan
=-3x^2

je me suis emballé en fait je vois pas..

malin,merci


mais y^2=√13/2 +3/2
x^2=√13/2 -3/2

on peut le résoudre ??...

ben j'obtiens x^4-x^2=-3

Que faire? x^2(x^2-1)+3=0

Bonjour à tous!
J'ai une équation
Z^2=-3-2i

Je pense qu'il n'y a pas de solution car Z^2 doit être positif

Sinon je fais Z^2=(x+yi)^2=-3-2i
j'arrive à x^2-y^2=-3 et y=-1/x mais à partir de la je m'en sors plus d’où ma première conclusion...

Une idée svp ??