Bonne continuation à toi
55 résultats trouvés
Revenir à la recherche avancée
Re: Redoubler dans une autre fac en ayant validé
Oui je pense que le mieux c'est de refaire une année , tu seras aussi plus a l'aise ça te permettra de te reposer un peu !
Bonne continuation à toi
Bonne continuation à toi
- 25 Jan 2018, 13:07
- Forum: ➳ Orientation
- Sujet: Redoubler dans une autre fac en ayant validé
- Réponses: 3
- Vues: 1485
Re: Présentation Omnubox
Bonjour chèr(e) collègue SIO,
Au plaisir d'échanger avec toi, bienvenu(e) et bonne continuation dans ton parcours
Au plaisir d'échanger avec toi, bienvenu(e) et bonne continuation dans ton parcours

- 23 Jan 2018, 09:46
- Forum: ✌ Présentez-vous
- Sujet: Présentation Omnubox
- Réponses: 1
- Vues: 302
Re: Redoubler dans une autre fac en ayant validé
Bonjour !
Je pense que tout dépend des modules. Comme tu le dis si bien, si se sont de bons Master, personnellement je redoublerai mon M1. Mais si tu fais une bonne M1 cette année, y a pas de raison pour que tu ne sois pas admis en M2 a Paris ?
Je pense que tout dépend des modules. Comme tu le dis si bien, si se sont de bons Master, personnellement je redoublerai mon M1. Mais si tu fais une bonne M1 cette année, y a pas de raison pour que tu ne sois pas admis en M2 a Paris ?

- 22 Jan 2018, 17:55
- Forum: ➳ Orientation
- Sujet: Redoubler dans une autre fac en ayant validé
- Réponses: 3
- Vues: 1485
Re: Suites
Regarde ce petit cours illustré, le principe est bien définit a la partie 2/ :
http://www.educastream.com/raisonnement ... erminale-s
http://www.educastream.com/raisonnement ... erminale-s
Re: Fonction et limite
Calcul très fastidieux mais on y arrives 







- 19 Jan 2018, 10:36
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
Re: Fonction et limite
Quand tu en es à l'étape : f'(x) = { [ (2x^2) / (2racinede(x^2+1)) ] - racinede(x^2+1) + 1 } * (1/x^2) Tu développes, c'est à dire : f'(x) = [ [ (2x^2) / (2racinede(x^2+1)) ] * (1/x^2) ] - [ racinede(x^2+1) * (1/x^2) ] + [ 1 * (1/x^2) ] Dans la partie en rouge c'est à dire cette partie : [ [ (2x^2) ...
- 19 Jan 2018, 10:31
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
Re: Fonction et limite
Tu dois trouver :
F'(x)=( racine(1+x^2) -1 ) / ( x^2 * racin(1+x^2) )
F'(x)=( racine(1+x^2) -1 ) / ( x^2 * racin(1+x^2) )
- 19 Jan 2018, 09:30
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
Re: Les suites
Par contre : S1n = ( (n+1)(-3n+4) )/2 S2n = - 1+2^n+1 Donc : Sn = [ ( (n+1)(-3n+4) )/2 ] + [ - 1+2^(n+1) ] Sn = [ ( (n+1)(-3n+4) )/2 ] - 1+2^(n+1) Maintenant il faut mettre sur le même dénominateur , donc tu multiplies la partie [ - 1+2^(n+1)] par 2 : Sn = ( (n+1)(-3n+4) - 2+2^(n+2) ) /2 Maintenant ...
- 18 Jan 2018, 10:24
- Forum: ✎✎ Lycée
- Sujet: Les suites
- Réponses: 22
- Vues: 1035
- 18 Jan 2018, 09:54
- Forum: ✎✎ Lycée
- Sujet: Géométrie et nombres complexes
- Réponses: 4
- Vues: 511
Re: Les suites
Pour la vérification tu as juste besoin de faire : 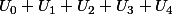
Et tu regardes si tu trouves le même résultat que quand tu fais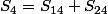
Et tu regardes si tu trouves le même résultat que quand tu fais
- 18 Jan 2018, 09:31
- Forum: ✎✎ Lycée
- Sujet: Les suites
- Réponses: 22
- Vues: 1035
Re: Fonction et limite
Oui c'est bien ça 
- 17 Jan 2018, 23:48
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
Re: Fonction et limite
N'oublies pas t'utiliser la règle : a/b = a* (1/b) , très utile pour quandtu as la division de deux fractions
- 17 Jan 2018, 19:22
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
Re: Fonction et limite
Dans ta fonction F(x) = [ ( Racine de x^2 +1)-1] / x Tu as : u(x) = Racinede(x^2 +1)-1 v(x) = x v(x)' = 1 u(x)' = 2x / 2 * racinede( x^2+1) ---> grace à (racine(u))′= u′ / (2 * racine(u)) v^2=x^2 du coup on remet tout dans l'ordre : f'(x) ={ [ (2x) / (2racinede(x^2+1))] * x - 1 * [racinede(x^2+1) - ...
- 17 Jan 2018, 19:20
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
Re: Présentation Zaal
Je te remercie Pascal16 !
Durant ma scolarité au lycée, je faisais du soutient scolaire aux collégiens. Avec mon école d'ingénieur, je manque de temps et ce forum me permet de continuer d'une autre façon, j'aime beaucoup l'approche !
Bonjour Pseuda,
Merci de l'avoir remarqué hehe
Durant ma scolarité au lycée, je faisais du soutient scolaire aux collégiens. Avec mon école d'ingénieur, je manque de temps et ce forum me permet de continuer d'une autre façon, j'aime beaucoup l'approche !
Bonjour Pseuda,
Merci de l'avoir remarqué hehe
- 17 Jan 2018, 18:33
- Forum: ✌ Présentez-vous
- Sujet: Présentation Zaal
- Réponses: 3
- Vues: 320
Re: Fonction et limite
Aller, dis moi ce que tu as fais/essayé pour le moment 
- 17 Jan 2018, 18:26
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
Re: Les suites
Si tu préfères ne pas développer, que c'est plus clair pour toi, tu peux rester à l'étape : s1n : (n+1)(-3n+4)/2 , ça ne change absolument rien pour le résultat.
Personnellement, je préfère enlever les parenthèses pour plus de visibilité.
Personnellement, je préfère enlever les parenthèses pour plus de visibilité.
- 17 Jan 2018, 18:09
- Forum: ✎✎ Lycée
- Sujet: Les suites
- Réponses: 22
- Vues: 1035
Re: Fonction et limite
Petit rappel :
(racine(u))′= u′ / (2 * racine(u))
Et :
(u/v)′= (u′v−uv′) / v²
Tu te souviens de ça ?
(racine(u))′= u′ / (2 * racine(u))
Et :
(u/v)′= (u′v−uv′) / v²
Tu te souviens de ça ?
- 17 Jan 2018, 17:59
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
Re: Les suites
Pour s2n : Oui oui désolée je divague aujourd'hui haha, c'est moche à lire les calcules linéaire comme ça.
Pour s1n par contre, :
((n+1)/2)*(uo+un)=((n+1)/2)*(4-3n) = (4n + 4 -3n² -3n)/2 = (-3n² -n + 4)/2
Pour s1n par contre, :
((n+1)/2)*(uo+un)=((n+1)/2)*(4-3n) = (4n + 4 -3n² -3n)/2 = (-3n² -n + 4)/2
- 17 Jan 2018, 17:46
- Forum: ✎✎ Lycée
- Sujet: Les suites
- Réponses: 22
- Vues: 1035
Re: Fonction et limite
Oui pardon pour mon inattention !
Et ne te sens pas obligé de me vouvoyer, je suis étudiante comme toi j'ai juste quelques années en plus
Et ne te sens pas obligé de me vouvoyer, je suis étudiante comme toi j'ai juste quelques années en plus
- 17 Jan 2018, 16:57
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
Re: Fonction et limite
OOUUPs oui pardon c'est bien ça  j'ai oublié le - devant ma racine hehe, au moins tu suis et tu as compris c'est ce qu'il faut !!
j'ai oublié le - devant ma racine hehe, au moins tu suis et tu as compris c'est ce qu'il faut !!
EDIT : J'ai rectifié
EDIT : J'ai rectifié
- 17 Jan 2018, 16:53
- Forum: ✎✎ Lycée
- Sujet: Fonction et limite
- Réponses: 58
- Vues: 1727
- 55 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
