Forum de Mathématiques: Maths-Forum

Bonjour, je rencontre quelques problèmes avec cet exercice d'algèbre : Énoncé : Soit E=\R^{\R} F l'ensemble des éléments de E de période 1 G l'ensemble des éléments de E de limite nulle en +\infty On admet que F et G sont SEV de E a) Démontrer que F \bigcap{G}={0_E} f=0 est élément de E, 1-périodiqu...

Bonjour, Pour b), à partir de f continue, comment peux-tu construire une fonction dans A facilement? Pour la c), ta première affirmation doit être complétée par et la fct nulle est continue et pour la deuxième, cela commence mal!! si f=0 alors F=0... J'ai été trop vite pour la c), j'ai corrigé: J'a...

Bonjour, je rencontre quelques difficultés face à l'exercice suivant : Exercice : Soit E l'espace des fonctions continues sur [0;1] à valeurs dans \R A = { f \in E, \int_{0}^{1}{f} = 0 }, B = {applications constantes de [0;1] dans \R } a) Montrer que A et B sont des SEV de E : aucun problème b) Mont...

Ahhh donc k(z) c'est le nombre de points existants vérifiant la propriété au temps pour moi je n'avais pas du tout compris l'énoncé, merci. Pour la première partie de la question 2, géométriquement, il se produit que le cercle autour des nombres est le même donc il contient autant de points pour les...

Bonjour, je rencontre des difficultés face à ce problème : Soit G l'ensemble des nombres complexes de la forme m+ni avec m et n entiers relatifs. A tout point z du plan complexes, on associe le nombre k(z) des points p de G tels que |z-p| < 1. 1°) Démonter que si la partie réelle x et la partie imag...

Bonjour, je bloque sur cet exercice où je ne comprends pas la question 2 : On considère l'équation d'inconnue X : X^5-X^3=n 1°) Montrer que pour tout entier naturel non nul n, il existe un unique réel strictement positif x_n vérifiant cette équation Pas de problème 2°) Montrer qu'il existe des const...

Avec ton exemple ça donne ça :
https://prnt.sc/m9pqqn
Donc l'idée serait de jouer sur la périodicité de la fonction pour montrer ça ? (ici pour a=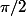, la tangente en coupe la courbe de f en () donc aussi en ()

Bonjour, j'ai du mal à comprendre cet exercice : Soit f de \R \rightarrow \R périodique et dérivable, et a \in \R . Montrer qu'il existe un réel x_0 tel que la tangente en x_0 au graphe de f coupe le graphe de f en (x_0+a;f(x_0+a)) Indication : on pourra utiliser le théorème de Darbo...

Merci pour vos réponses. Voilà ce que j'obtiens pour la b : Soit g : E' \rightarrow F' Construisons f : E \rightarrow F telle que v\circ f\circ u=g Soit y \in F' . v est surjective donc il existe z_y \in F, v(z_y) = y . On pose \forall x \in E', y=g(x) Soit (x'...

Bonjour, je suis confronté à un exercice sur les applications : Soient E, E', F, F' quatre ensembles. Soient les applications : u: E' -> E v : F -> F' \Phi : F^E \rightarrow F'^{E'} définie par \forall f \in F^E, \Phi(f) = vofou a) Si u est surjective et v injective, alors \Phi est i...

Si ce n'était pas le cas, il existerait un élément x de F sans antécédent par f. On aurait alors g(F)=g(F-{x}) impossible puisque g est injective donc f est surjective c'est analogue dans l'autre sens comme x n'a pas d'antécédent, l'ensemble des antécédents de F est bien égal à l'ensemble des antéc...

Merci de vos réponses. salut Juste une petite contribution pour le 1 On suppose que g est injective. Montrons que f est surjective. Si ce n'était pas le cas, il existerait un élément x de F sans antécédent par f. On aurait alors g(F)=g(F-{x}) impossible puisque g est injective donc f est surjective ...

Bonjour, j'ai du mal à résoudre cet exercice sur les ensembles, applications et images réciproques : Soit f une application de E dans F. On définit l'application g : P(F) -> P(E) par : \forall Y \subset F, g(Y) = f^{-1}(Y) 1.Montrer que g est injective si et seulement si f est surjec...

Merci pour ta réponse encore une fois ! Je te donne la dernière partie et mes recherches (et j'édit le post initial) : 4. Étude d'un cas particulier. On suppose toujours que f = \frac{1}{2}sin , et on suppose de plus que u_0 = \frac{\pi}{6}, u_1 = \frac{1}{4} . (a) Justifier que pour tout entier nat...

Voici la suite du problème : On s'intéresse maintenant au cas où f est donné par f : x -> \frac{1}{2} sin(x) 3. Étude générale de la suite définie par : \forall n \geq 0, u_{n+2} = \frac{1}{2} sin(\frac{u_{n+1}+\frac{1}{2}sin(u_n)}{2}) (a) Montrer que [0;1] est stable par f :...

Merci Vu que tu sait déjà que u_1 et f(u_0) sont dans I , le truc dont tu as besoin, c'est de montrer que si deux réels a et b sont dans I alors \dfrac{a+b}{2} est lui aussi dans I . Et c'est évidement vrai vu que I est un intervalle ce qui implique que, s'il contient a et b alors il contien...

Bonjour, j'ai du mal à résoudre ce problème sur les suites définies par récurrence : Les questions où j'ai encore besoin d'aide sont en rouge , celles qui ont déjà été résolues sont en noires L'objet de cet exercice est l'étude des suites définies par une récurrence du type u_{n+2} = f(\frac{u_{...

Merci, j'ai pu finir la Q1. Voici la question 2 à laquelle je rencontre également quelques problèmes : Q2) Dans cette question, on se place sur l'intervalle J = ] -\infty ; 0 [ . On pose z(x) = \frac{y(x)}{x^3} et Z = z' a) Montrer que y est solution de (E) sur J <=> \forall x < 0, x...

Il y'a une autre méthode proposée question 3 mais je n'y suis pas encore Voilà ce que j'ai pour la question 1.b), est-ce correct ? b) Résoudre soigneusement l'équation (E') et donner les solutions réelles pour g. L'équation homogène associée à (E') est : (H') \forall t \in \R, g''(t)...

LB2 a écrit:Non, tu t'es trompé dans l'expression de g'(t) : il faut dériver (vou) avec v=y et u=exp
Je te rappelle que (vou)'=u'*v'ou

Ah oui pardon, ça donne : donc :