Forum de Mathématiques: Maths-Forum

Soit une fonction vérifiant . Supposons intégrable au sens de Lebesgue sur chaque intervalle compact de . Montrer que est linéaire ?
Quelqu'un peut-il m'aider pour résoudre ce problème ?
Merci beaucoup

Ok merci bien,
La suite du problème est :
montrer que F est continue.
je ne comprend pas car une fonction en escalier n'est pas continue mais est Lebesgue intégrable

Bonjour
Voila ma question :
Soit intégrable au sens de Lebesgue:
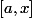
Justifier que est Lebesgue intégrable sur tout interalle où
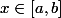
Quelqu'un aurait-il une idée de solution ?
Merci d'avance